See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below
★ See also the PDF version of this chapter (better formatting/references) ★
Hash Functions, Random Oracles, and Bitcoin
We have seen pseudorandom generators, functions and permutations, as well as Message Authentication codes, CPA and CCA secure encryptions. This week we will talk about cryptographic hash functions and some of their magical properties. We motivate this by the Bitcoin cryptocurrency. As usual our discussion will be highly abstract and idealized, and any resemblance to real cryptocurrencies, living or dead, is purely coincidental.
The “Bitcoin” Problem
Using cryptography to create a centralized digital-currency is fairly straightforward, and indeed this is what is done by Visa, Mastercard, and so on. The main challenge with Bitcoin is that it is decentralized. There is no trusted server, there are no “user accounts”, no central authority to adjudicate claims. Rather we have a collection of anonymous and autonomous parties that somehow need to agree on what is a valid payment.
The Currency Problem
Before talking about cryptocurrencies, let’s talk about currencies in general.1 At an abstract level, a currency requires two components:
A scarce resource.
A mechanism for determining and transferring ownership of certain quantities of this resource.
Some currencies are/were based on commodity money. The scarce resource was some commodity having intrinsic value, such as gold or silver, or even salt or tea, and ownership based on physical possession. However, for various financial and political reasons, some societies shifted to representative money, where the currency is not the commodity itself but rather a certificate that provides the right to the commodity. Representative money requires trust in some central authority that would respect the certificate. The next step in the evolution of currencies was fiat money, which is a currency (like today’s dollar, ever since the U.S. moved off the gold standard) that does not correspond to any commodity, but rather only relies on trust in a central authority. (Another example is the Roman coins, which though originally made of silver, underwent a continous process of debasement until they contained less than two percent of it.) One advantage (sometimes disadvantage) of a fiat currency is that it allows for more flexible monetary policy on parts of the central authority.
Bitcoin Architecture
Bitcoin is a fiat currency without a central authority. A priori this seems like a contradiction in terms. If there is no trusted central authority, how can we ensure a scarce resource? Who settles claims of ownership? And who sets monetary policy?
For instance, one problem we are particularly concerned with is the double-spend problem. The following scenario is a double-spend:
- Adversary \(A\) orders a pizza from Pinocchio’s.
- \(A\) gives Pinocchio’s a particular “set” of money \(m\).
- \(A\) eats the pizza.
- \(A\) gives that same set of money \(m\) to another Domino’s such that Pinocchio’s no longer has that money.
- \(A\) eats the second pizza.
With cash, this situation is unfathomable. But think about a credit card: if you can “revoke” (or dispute) the first payment, you could take money away from Pinocchio’s after you’ve received some goods or services. Also consider that rather than giving \(m\) to Domino’s in step 4, \(A\) could just give \(m\) back to itself.
We want to make it difficult or impossible for the anyone to perform a double-spend like this.
Bitcoin (and other cryptocurrencies) aims to provide cryptographic solutions to this problem and more.
The basic unit in the Bitcoin system is a coin. Each coin has a unique identifier, and a current owner .2 Transactions in the system have either the form of “mint coin with identifier \(\ensuremath{\mathit{ID}}\) and owner \(P\)” or “transfer the coin \(\ensuremath{\mathit{ID}}\) from \(P\) to \(Q\)”. All of these transactions are recorded in a public ledger.
Since there are no user accounts in Bitcoin, the “entities” \(P\) and \(Q\) are not identifiers of any physical person. Rather \(P\) and \(Q\) are “computational puzzles”. A computational puzzle can be thought of as a string \(\alpha\) that specifies some “problem” such that it’s easy to verify whether some other string \(\beta\) is a “solution” for \(\alpha\), but it is hard to find such a solution on your own. (Students with complexity background will recognize here the class NP.) So when we say “transfer the coin \(\ensuremath{\mathit{ID}}\) from \(P\) to \(Q\)” we mean that whomever holds a solution for the puzzle \(Q\) is now the owner of the coin \(\ensuremath{\mathit{ID}}\) (and to verify the authenticity of this transfer, you provide a solution to the puzzle \(P\).) More accurately, a transaction involving the coin \(\ensuremath{\mathit{ID}}\) is self-validating if it contains a solution to the puzzle that is associated with \(\ensuremath{\mathit{ID}}\) according to the latest transaction in the ledger.
Please re-read the previous paragraph, to make sure you follow the logic.
One theoretical example of a puzzle is the following: if \(N\) is the puzzle, an entity can “prove” that they own coins assigned to \(N\) if they can produce numbers \(A,B\) such that \(N=A\cdot B\).
Another more generic example (that you can keep in mind as a potential implementation for the puzzles we use here) is: \(\alpha\) is some string in \(\{0,1\}^{2n}\) and \(\beta\) will be a string in \(\{0,1\}^n\) such that \(\alpha = G(\beta)\) where \(G:\{0,1\}^n\rightarrow\{0,1\}^{2n}\) is some pseudorandom generator.
The real Bitcoin system typically uses puzzles based on digital signatures, a concept we will learn about later in this course, but you can simply think of \(P\) as specifying some abstract puzzle and every person that can solve \(P\) can construct transactions with the coins owned by \(P\).3 Unfortunately, this means if you lose the solution to the puzzle then you have no access to the coin. More alarmingly, if someone steals the solution from you, then you have no recourse or way to get your coin back. People have managed to lose millions of dollars in this way.
The Bitcoin Ledger
The main idea behind Bitcoin is that there is a public ledger that contains an ordered list of all the transactions that were ever performed and are considered as valid in the system. Given such a ledger, it is easy to answer the question of who owns any particular coin. The main problem is how does a collection of anonymous parties without any central authority agree on this ledger? This is an instance of the consensus problem in distributed computing. This seems quite scary, as there are very strong negative results known for this problem; for example the famous Fischer, Lynch, Patterson (FLP) result showed that if there is even one party that has a benign failure (i.e., it halts and stop responding) then it is impossible to guarantee consensus in a completely asynchronous network. Things are better if we assume some degree of partial synchrony (i.e., a global clock and some bounds on the latency of messages) as well as that a majority or supermajority of the parties behave correctly.
The partial synchrony assumption is typically approximately maintained on the Internet, but the honest majority assumption seems quite suspicious. What does it mean a “majority of parties” in an anonymous network where a single person can create multiple “entities” and cause them to behave arbitrarily maliciously (known as “byzantine” faults in distributed parlance)? Also, why would we assume that even one party would behave honestly- if there is no central authority and it is profitable to cheat then everyone would cheat, wouldn’t they?

Perhaps the main idea behind Bitcoin is that “majority” will correspond to a “majority of computing power”, or as the original Bitcoin paper says, “one CPU one vote” (or perhaps more accurately, “one cycle one vote”). It might not be immediately clear how to implement this, but at least it means that creating fictitious new entities (sometimes known as a Sybil attack after the movie about multiple-personality disorder) cannot help. To implement it we turn to a cryptographic concept known as “proof of work” which was originally suggested by Dwork and Naor in 1991 as a way to combat mass marketing email.4
Consider a pseudorandom function \(\{ f_k \}\) mapping \(n\) bits to \(\ell\) bits. On average, it will take a party Alice \(2^\ell\) queries to obtain an input \(x\) such that \(f_k(x)=0^\ell\). So, if we’re not too careful, we might think of such an input \(x\) as a proof that Alice spent \(2^\ell\) time.
Stop here and try to think if indeed it is the case that one cannot find an input \(x\) such that \(f_k(x)=0^\ell\) using much fewer than \(2^\ell\) steps.
The main question in using PRF’s for proofs of work is who is holding the key \(k\) for the pseudorandom function. If there is a trusted server holding the key, then sure, finding such an input \(x\) would take on average \(2^\ell\) queries, but the whole point of Bitcoin is to not have a trusted server. If we give \(k\) to a party Alice, then can we guarantee that she can’t find a “shortcut” to find such an input without running \(2^\ell\) queries? The answer, in general, is no.
Indeed, it is an excellent exercise to prove that (under the PRF conjecture) that there exists a PRF \(\{ f_k \}\) mapping \(n\) bits to \(n\) bits and an efficient algorithm \(A\) such that \(A(k)=x\) such that \(f_k(x)=0^\ell\).
However, suppose that \(\{ f_k \}\) was somehow a “super-strong PRF” that would behave like a random function even to a party that holds the key. In this case, we can imagine that making a query to \(f_k\) corresponds to tossing \(\ell\) independent random coins, and it would not be feasible to obtain \(x\) such that \(f_k(x)=0^\ell\) using much less than \(2^\ell\) cycles. Thus presenting such an input \(x\) can serve as a “proof of work” that you’ve spent \(2^\ell\) cycles or so. By adjusting \(\ell\) we can obtain a proof of spending \(T\) cycles for a value \(T\) of our choice. Now if things would go as usual in this course then I would state a result like the following:
Theorem: Under the PRG conjecture, there exist super strong PRF.
Where again, the “super strong PRF” behaves like a truly random function even to a party that holds the key. Unfortunately such a result is not known to be true, and for a very good reason. Most natural ways to define “super strong PRF” will result in properties that can be shown to be impossible to achieve. Nevertheless, the intuition behind it still seems useful and so we have the following heuristic:
The random oracle heuristic (aka “Random oracle model”, Bellare-Rogaway 1993): If a “natural” protocol is secure when all parties have access to a random function \(H:\{0,1\}^n\rightarrow\{0,1\}^\ell\), then it remains secure even when we give the parties the description of a cryptographic hash function with the same input and output lengths.
We don’t have a good characterization as to what makes a protocol “natural” and we do have fairly strong counterexamples to this heuristic (though they are arguably “unnatural”). That said, it still seems useful as a way to get intuition for security, and in particular to analyze Bitcoin (and many other practical protocols) we do need to assume it, at least given current knowledge.
The random oracle heuristic is very different from all the conjectures we considered before. It is not a formal conjecture since we don’t have any good way to define “natural” and we do have examples of protocols that are secure when all parties have access to a random function but are insecure whenever we replace this random function by any efficiently computable function (see the homework exercises).
Under the random oracle model, we can now specify the “proof of work” protocol for Bitcoin. Given some identifier \(\ensuremath{\mathit{ID}}\in\{0,1\}^n\), an integer \(T \ll 2^n\), and a hash function \(H:\{0,1\}^{2n}\rightarrow\{0,1\}^n\), the proof of work corresponding to \(\ensuremath{\mathit{ID}}\) and \(T\) will be some \(x\in\{0,1\}^*\) such that the first \(\lceil \log T \rceil\) bits of \(H(\ensuremath{\mathit{ID}}\| x)\) are zero.5
From Proof of Work to Consensus on Ledger
How does proof of work help us in achieving consensus?
We want every transaction \(t_i\) in the Bitcoin system to have a corresponding proof of work. In particular, some proof of \(T_i\) time “amount” of work with respect to some identifier that is unique to \(t_i\).
The length of a ledger \((t_1,\ldots,t_n)\) is the sum of the corresponding \(T_i\)’s. In other words, the length corresponds to the total number of cycles invested in creating this ledger. A ledger is valid if every transaction in the ledger of the form “transfer the coin \(\ensuremath{\mathit{ID}}\) from \(P\) to \(Q\)” is self-certified by a solution to \(P\).
Critically, participants (specifically miners) in the Bitcoin network are rewarded for adding valid entries to the ledger. In other words, they are given Bitcoins (which are newly minted for them) for performing the “work” required to add an entry to the ledger. However, honest participants (including non-miners, people who just read the ledger) will accept the longest known ledger as the ground truth. In addition, Bitcoin miners are rewarded for adding entry \(i\) after entry \(i+100\) is added to the ledger. This gives miners an incentive to choose the longest ledger to contribute their work towards. To see why, consider the following rough approximation of the incentive structure:
Remember that Bitcoin miners are rewarded for adding entry \(i\) after entry \(i+100\) is added to the ledger. Thus, by spending “work” (which directly corresponds to CPU cycles, which directly corresponds to monetary value), miners are “betting” on whether a particular ledger will “win”. Think of yourself as a miner, and consider a scenario in which there are two competing ledgers. Ledger 1 has length \(3\) and Ledger 2 has length \(6\). That means miners have put roughly 2x the amount of work (= CPU cycles = money) into Ledger 2. In order for Ledger 1 to “win” (from your perspective that means reach length \(104\) to claim your prize and to become longer than Ledger 2), you would have to perform \(3\) entries worth of work just to get Ledger 1 to length \(6\). But in the meantime, other miners will already be working on Ledger 2, further increasing its length! Thus you want to add entries to Ledger 2.
If a ledger \(L\) corresponds to the majority of the cycles that were available in this network then every honest party would accept it, as any alternative ledger would be necessarily shorter. (See Figure 7.1.)
Thus one can hope that the consensus ledger will continue to grow. (This is a rather hand-wavy and imprecise argument, see this paper for a more in depth analysis; this is also related to the phenomenon known as preferential attachment.)
Cost to mine, mining pools: Generally, if you know that completing a \(T\)-cycle proof will get you a single coin, then making a single query (which will succeed with probability \(1/T\)) is akin to buying a lottery ticket that costs you a single cycle and has probability \(1/T\) to win a single coin. One difference over the actual lottery is that there is also some probability that you’re working on the wrong fork of the ledger, but this incentivizes people to avoid this as much as possible. Another, perhaps even more major difference, is that things are setup so that this is a profitable enterprise and the cost of a cycle is smaller than the value of \(1/T\) coins. Just like in the lottery, people can and do gather in groups (known as “mining pools”) where they pool together all their computing resources, and then split the award if they win it. Joining a pool doesn’t change your expectation of winning but reduces the variance. In the extreme case, if everyone is in the same pool, then for every cycle you spend you get exactly \(1/T\) coins. The way these pools work in practice is that someone that spent \(C\) cycles looking for an output with all zeroes, only has probability \(C/T\) of getting it, but is very likely to get an output that begins with \(\log C\) zeroes. This output can serve as their own “proof of work” that they spent \(C\) cycles and they can send it to the pool management so they get an appropriate share of the reward.
The real Bitcoin: There are several aspects in which the protocol described above differs from the real Bitcoin protocol. Some of them were already discussed above: Bitcoin typically uses digital signatures for puzzles (though it has a more general scripting language to specify them), and transactions involve a number of Satoshis (and the user interface typically displays currency is in units of BTC which are \(10^8\) Satoshis). The Bitcoin protocol also has a formula designed to factor in the decrease in dollar cost per cycle so that Bitcoins become more expensive to mine with time. There is also a fee mechanism apart from the mining to incentivize parties to add to the ledger. (The issue of incentives in Bitcoin is quite subtle and not fully resolved, and it is possible that parties’ behavior will change with time.) The ledger does not grow by a single transaction at a time but rather by a block of transactions, and there is also some timing synchronization mechanism (which is needed, as per the consensus impossibility results). There are other differences as well; see the Bonneau et al paper as well as the Tschorsch and Scheuermann survey for more.
Collision Resistance Hash Functions and Creating Short “Unique” Identifiers
Another issue we “swept under the carpet” is how do we come up with these unique identifiers per transaction. We want each transaction \(t_i\) to be bound to the ledger state \((t_1,\ldots,t_{i-1})\), and so the ID of \(t_i\) should contain also the ID’s all the prior transactions. But yet we want this ID to be only \(n\) bits long. Ideally, we could solve this if we had a one to one mapping \(H\) from \(\{0,1\}^N\) to \(\{0,1\}^n\) for some very large \(N\gg n\). Then the ID corresponding to the task of appending \(t_i\) to \((t_1,\ldots,t_{i-1})\) would simply be \(H(t_1\|\cdots\|t_i)\). The only problem is that this is of course clearly impossible- \(2^N\) is much bigger than \(2^n\) and there is no one to one map from a large set to a smaller set. Luckily we are in the magical world of crypto where the impossible is routine and the unimaginable is occasional. So, we can actually find a function \(H\) that is “essentially” one to one.
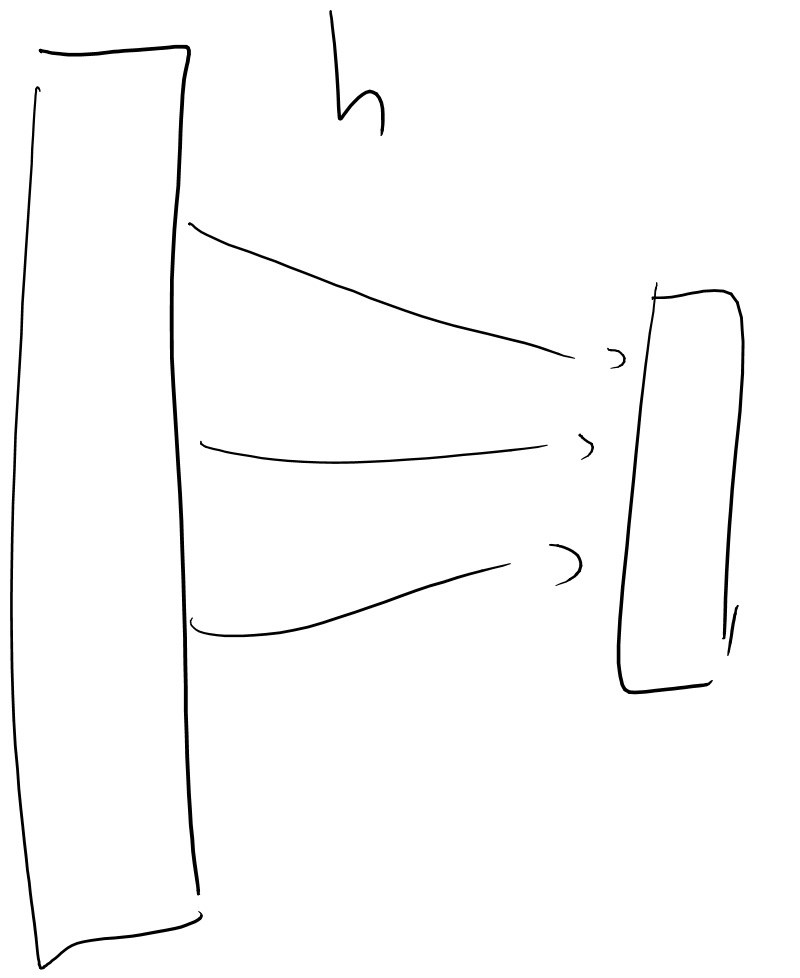
The main idea is the following simple result, which can be thought of as one side of the so called “birthday paradox”:
If \(H\) is a random function from some domain \(S\) to \(\{0,1\}^n\), then the probability that after \(T\) queries an attacker finds \(x\neq x'\) such that \(H(x)=H(x')\) is at most \(T^2/2^n\).
Let us think of \(H\) in the “lazy evaluation” mode where for every query the adversary makes, we choose a random answer in \(\{0,1\}^n\) at the time it is made. (We can assume the adversary never makes the same query twice since a repeat query can be simulated by repeating the same answer.) For \(i< j\) in \([T]\) let \(E_{i,j}\) be the event that \(H(x_i)=H(x_j)\). Since \(H(x_j)\) is chosen at random and independently from the prior choice of \(H(x_i)\), the probability of \(E_{i,j}\) is \(2^{-n}\). Thus the probability of the union of \(E_{i,j}\) over all \(i,j\)’s is less than \(T^2/2^n\), but this probability is exactly what we needed to calculate.
This means that a random function \(H\) is collision resistant in the sense that it is hard for an efficient adversary to find two inputs that collide. Thus the random oracle heuristic would suggest that a cryptographic hash function can be used to obtain the following object:
A collection \(\{ h_k \}\) of functions where \(h_k:\{0,1\}^*\rightarrow\{0,1\}^n\) for \(k\in\{0,1\}^n\) is a collision resistant hash function (CRH) collection if the map \((k,x)\mapsto h_k(x)\) is efficiently computable and for every efficient adversary \(A\), the probability over \(k\) that \(A(k)=(x,x')\) such that \(x\neq x'\) and \(h_k(x)=h_k(x')\) is negligible.6
Once more we do not know a theorem saying that under the PRG conjecture there exists a collision resistant hash function collection, even though this property is considered as one of the desiderata for cryptographic hash functions. However, we do know how to obtain collections satisfying this condition under various assumptions that we will see later in the course such as the learning with error problem and the factoring and discrete logarithm problems. Furthermore if we consider the weaker notion of security under a second preimage attack (also known as being a “universal one way hash function” or UOWHF) then it is known how to derive such a function from the PRG assumption.
A collection \(\{ h_k \}\) of collision resistant hash functions is an incomparable object to a collection \(\{ f_s \}\) of pseudorandom functions with the same input and output lengths. On one hand, the condition of being collision-resistant does not imply that \(h_k\) is indistinguishable from random. For example, it is possible to construct a valid collision resistant hash function where the first output bit always equals zero (and hence is easily distinguishable from a random function). On the other hand, unlike Definition 4.1, the adversary of Definition 7.3 is not merely given a “black box” to compute the hash function, but rather the key to the hash function. This is a much stronger attack model, and so a PRF does not have to be collision resistant. (Constructing a PRF that is not collision resistant is a nice and recommended exercise.)
Practical Constructions of Cryptographic Hash Functions
While we discussed hash functions as keyed collections, in practice people often think of a hash function as being a fixed keyless function. However, this is because most practical constructions involve some hardwired standardized constants (often known as IV) that can be thought of as a choice of the key.
Practical constructions of cryptographic hash functions start with a basic block which is known as a compression function \(h:\{0,1\}^{2n}\rightarrow\{0,1\}^n\). The function \(H:\{0,1\}^*\rightarrow\{0,1\}^n\) is defined as \(H(m_1,\ldots,m_t)=h(h(h(m_1,\ensuremath{\mathit{IV}}),m_2),\cdots,m_t)\) when the message is composed of \(t\) blocks (and we can pad it otherwise). See Figure 7.3. This construction is known as the Merkle-Damgard construction and we know that it does preserve collision resistance:
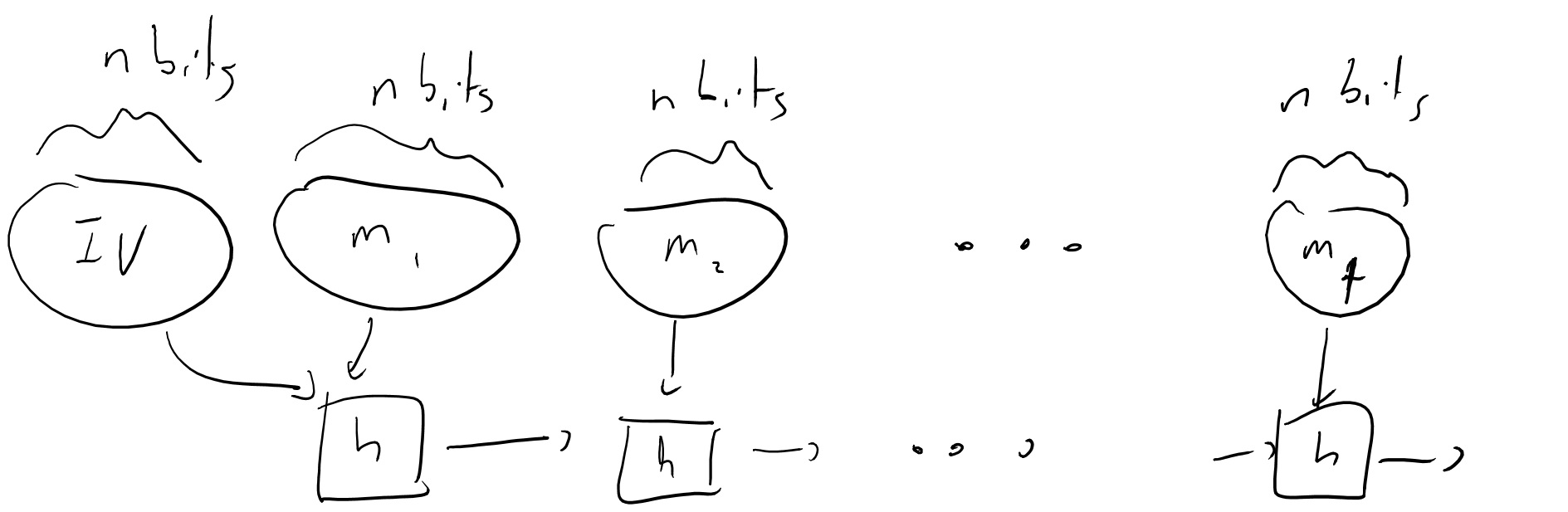
Let \(H\) be constructed from \(h\) as above. Then given two messages \(m \neq m' \in \{0,1\}^{tn}\) such that \(H(m)=H(m')\) we can efficiently find two messages \(x \neq x' \in \{0,1\}^{2n}\) such that \(h(x)=h(x')\).
The intuition behind the proof is that if \(h\) was invertible then we could invert \(H\) by simply going backwards. Thus in principle if a collision for \(H\) exists then so does a collision for \(h\). Now of course this is a vacuous statement since both \(h\) and \(H\) shrink their inputs and hence clearly have collisions. But we want to show a constructive proof for this statement that will allow us to transform a collision in \(H\) to a collision in \(h\). This is very simple. We look at the computation of \(H(m)\) and \(H(m')\) and at the first block in which the inputs differ but the output is the same (there must be such a block). This block will yield a collision for \(h\).
Practical Random-ish Functions
In practice we want much more than collision resistance from our hash functions. In particular we often would like them to be PRF’s as well. Unfortunately, the Merkle-Damgard construction is not a PRF even when \(\ensuremath{\mathit{IV}}\) is random and secret. This is because we can perform a length extension attack on it. Even if we don’t know \(\ensuremath{\mathit{IV}}\), given \(y=H_{IV}(m_1,\ldots,m_t)\) and a block \(m_{t+1}\) we can compute \(y' = h(y,m_{t+1})\) which equals \(H_{IV}(m_1,\ldots,m_{t+1})\).
One fix for this is to use a different \(\ensuremath{\mathit{IV}}'\) in the end of the encryption. That is, we define:
\(H_{IV,\ensuremath{\mathit{IV}}'}(m_1,\ldots,m_t) = h(\ensuremath{\mathit{IV}}',H_{IV}(m_1,\ldots,m_t))\)
A variant of this construction (where \(\ensuremath{\mathit{IV}}'\) is obtained as some simple function of \(\ensuremath{\mathit{IV}}\)) is known as HMAC and it can be shown to be a pseudorandom function under some pseudorandomness assumptions on the compression function \(h\). It is very widely implemented. In many cases where I say “use a cryptographic hash function” in this course I actually mean to use an HMAC like construction that can be conjectured to give at least a PRF if not stronger “random oracle”-like properties.
The simplest implementation for a compression function is to take a block cipher with an \(n\) bit key and an \(n\) bit message and then simply define \(h(x_1,\ldots,x_{2n})=E_{x_{n+1},\ldots,x_{2n}}(x_{1},\ldots,x_{n})\). A more common variant is known as Davies-Meyer where we also XOR the output with \(x_{n+1},\ldots x_{2n}\). In practice people often use tailor made block ciphers that are designed for some efficiency or security concerns.
Some History
Almost all practically used hash functions are based on the Merkle-Damgard paradigm. Hash functions are designed to be extremely efficient7 which also means that they are often at the “edge of insecurity” and indeed have fallen over the edge.
In 1990 Ron Rivest proposed MD4, which was already showing weaknesses in 1991, and a full collision was found in 1995. Even faster attacks have been since found and MD4 is considered completely insecure.
In response to these weaknesses, Rivest designed MD5 in 1991. A weakness was shown for it in 1996 and a full collision was shown in 2004. Hence it is now also considered insecure.
In 1993 the National Institute of Standards proposed a standard for a hash function known as the Secure Hash Algorithm (SHA), which had quite a few similarities with the MD4 and MD5 functions. This function was known as SHA-0, and the standard was replaced in 1995 with SHA-1, which includes an extra “mixing” (i.e., bit rotation) operation. At the time no explanation was given for this change, but SHA-0 was later found to be insecure. In 2002 a variant with longer output, known as SHA-256, was added (as well as some others). In 2005, following the MD5 collision, significant weaknesses were shown in SHA-1. In 2017, a full SHA-1 collision was found. Today SHA-1 is considered insecure and SHA-256 is recommended.
Given the weaknesses in MD-5 and SHA-1, NIST started a competition in 2006 for a new hashing standard, based on functions that seem sufficiently different from the MD5/SHA-0/SHA-1 family. (SHA-256 is unbroken but it seems too close for comfort to those other systems.) The hash function Keccak was selected as the new standard SHA-3 in August of 2015.
The NSA and Hash Functions
The NSA is the world’s largest employer of mathematicians, and is very heavily invested in cryptographic research. It seems quite possible that they devote far more resources to analyzing symmetric primitives such as block ciphers and hash functions than the open research community. Indeed, the history above suggests that the NSA has consistently discovered attacks on hash functions before the cryptographic community (and the same holds for the differential cryptanalysis technique for block ciphers). That said, despite the “mythic” powers that are sometimes ascribed to the NSA, this history suggests that they are ahead of the open community, but not so much ahead, discovering attacks on hash functions about 5 years or so before they appear in the open literature.
There are a few ways we can get “insider views” to the NSA’s thinking. Some such insights can be obtained from the Snowden documents. The Flame malware was discovered in Iran in 2012 after operating since at least 2010. It used an MD5 collision to achieve its goals. Such a collision was known in the open literature since 2008, but Flame used a different variant that was unknown in the literature. For this reason it is suspected that it was designed by a western intelligence agency.
Another insight into NSA’s thoughts can be found in pages 12-19 of NSA’s internal Cryptolog newsletter which was recently declassified; one can find there a rather entertaining and opinionated (or obnoxious, depending on your point of view) review of the CRYPTO 1992 conference. In page 14 the author remarks that certain weaknesses of MD5 demonstrated in the conference are unlikely to be extended to the full version, which suggests that the NSA (or at least the author) was not aware of the MD5 collisions at the time. (The full archive of the cryptolog newsletter makes for some interesting reading!)
Cryptographic vs Non-Cryptographic Hash Functions
Hash functions are of course also widely used for non-cryptographic applications such as building hash tables and load balancing. For these applications people often use linear hash functions known as cyclic redundancy codes (CRC). Note however that even in those seemingly non-cryptographic applications, an adversary might cause significant slowdown to the system if he can generate many collisions. This can and has been used to obtain denial of service attacks. As a rule of thumb, if the inputs to your system might be generated by someone who does not have your best interests at heart, you’re better off using a cryptographic hash function.
Reading comprehension exercises
I recommend students do the following exercises after reading the lecture. They do not cover all material, but can be a good way to check your understanding.
Choose the strongest true statement from the following options. (That is, choose the mathematical statement from these options that is both true, and one can derive the other true statements as direct corollaries.)
For every function \(h:\{0,1\}^{1024} \rightarrow \{0,1\}^{128}\) there exist two strings \(x \neq x'\) in \(\{0,1\}^{1024}\) such that \(h(x)=h(x')\).
There is a randomized algorithm \(A\) that makes at most \(2^{128}\) queries to a given black box computing a function \(h:\{0,1\}^{1024} \rightarrow \{0,1\}^{128}\) that with probability at least \(0.9\), \(A\) outputs a pair \(x \neq x'\) in \(\{0,1\}^{1024}\) such that \(h(x)=h(x')\).
There is a randomized algorithm \(A\) that makes at most \(100 \cdot 2^{64}\) queries to a given black box computing a function \(h:\{0,1\}^{1024} \rightarrow \{0,1\}^{128}\) that with probability at least \(0.9\), \(A\) outputs a pair \(x \neq x'\) in \(\{0,1\}^{1024}\) such that \(h(x)=h(x')\).
There is a randomized algorithm \(A\) that makes at most \(0.01 \cdot 2^{64}\) queries to a given black box computing a function \(h:\{0,1\}^{1024} \rightarrow \{0,1\}^{128}\) that with probability at least \(0.9\), \(A\) outputs a pair \(x \neq x'\) in \(\{0,1\}^{1024}\) such that \(h(x)=h(x')\).
Suppose that \(h:\{0,1\}^{1024} \rightarrow \{0,1\}^{128}\) is chosen at random. If \(y\) is chosen at random in \(\{0,1\}^{128}\) and we pick \(x_1,\ldots,x_t\) independently at random in \(\{0,1\}^{1024}\), how large does \(t\) need to be so that the probability that there is some \(x_i\) such that \(h(x_i)=y\) is at least \(1/2\). (Pick the answer with the closest estimate):
\(2^{1024}\)
\(2^{256}\)
\(2^{128}\)
\(2^{64}\)
Suppose that a message authentication code \((S,V)\) where Alice and Bob use as one of its components a function \(h\) as a black box is secure when \(h\) is a random function. Is it still secure when Alice and Bob uses a hash function \(h\) that is chosen from some PRF collection and whose key is given to the adversary?
It can sometimes be secure and sometimes insecure.
It is always secure.
It is always insecure.
- ↩
I am not an economist by any stretch of the imagination, so please take the discussion below with a huge grain of salt. I would appreciate any comments on it.
- ↩
This is one of the places where we simplify and deviate from the actual Bitcoin system. In the actual Bitcoin system, the atomic unit is known as a Satoshi and one Bitcoin (abbreviated BTC) is \(10^8\) Satoshis. For reasons of efficiency, there is no individual identifier per Satoshi and transactions can involve transfer and creation of multiple Satoshis. However, conceptually we can think of atomic coins each of which has a unique identifier.
- ↩
There are reasons why Bitcoin uses digital signatures and not these puzzles. The main issue is that we want to bind the puzzle not just to the coin but also to the particular transaction, so that if you know the solution to the puzzle \(P\) corresponding to the coin \(\ensuremath{\mathit{ID}}\) and want to use that to transfer it to \(Q\), it won’t be possible for someone to take your solution and use that to transfer the coin to \(Q'\) before your transaction is added to the public ledger. We will come back to this issue after we learn about digital signatures. As a quick preview, in Bitcoin the puzzle is as follows: whoever can produce a digital signature with the private key corresponding to the public key \(P\) can claim these coins.
- ↩
This was a rather visionary paper in that it foresaw this issue before the term “spam” was introduced and indeed when email itself, let alone spam email, was hardly widespread.
- ↩
The actual Bitcoin protocol is slightly more general, where the proof is some \(x\) such that \(H(\ensuremath{\mathit{ID}}\|x)\), when interpreted as a number in \([2^n]\), is at most \(T\). There are also other issues about how exactly \(x\) is placed and \(\ensuremath{\mathit{ID}}\) is computed from past history that we ignore here.
- ↩
Note that the other side of the birthday bound shows that you can always find a collision in \(h_k\) using roughly \(2^{n/2}\) queries. For this reason we typically need to double the output length of hash functions compared to the key size of other cryptographic primitives (e.g., \(256\) bits as opposed to \(128\) bits).
- ↩
For example, the Boneh-Shoup book quotes processing times of up to 255MB/sec on a 1.83 Ghz Intel Core 2 processor, which is more than enough to handle not just Harvard’s network but even Lamar College’s.
Comments
Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.
Compiled on 11/17/2021 22:36:30
Copyright 2021, Boaz Barak.

This work is
licensed under a Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Produced using pandoc and panflute with templates derived from gitbook and bookdown.