See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below
★ See also the PDF version of this chapter (better formatting/references) ★
Concrete candidates for public key crypto
In the previous lecture we talked about public key cryptography and saw the Diffie Hellman system and the DSA signature scheme. In this lecture, we will see the RSA trapdoor function and how to use it for both encryptions and signatures.
Some number theory.
(See Shoup’s excellent and freely available book for extensive coverage of these and many other topics.)
For every number \(m\), we define \(\Z_m\) to be the set \(\{0,\ldots,m-1\}\) with the addition and multiplication operations modulo \(m\). When two elements are in \(\Z_n\) then we will always assume that all operations are done modulo \(m\) unless stated otherwise. We let \(\Z^*_m = \{ a\in \Z_m : gcd(a,m)=1 \}\). Note that \(m\) is prime if and only if \(|\Z^*_m|=m-1\). For every \(a \in \Z^*_m\) we can find using the extended gcd algorithm an element \(b\) (typically denoted as \(a^{-1}\)) such that \(ab=1\) (can you see why?). The set \(\Z^*_m\) is an abelian group with the multiplication operation, and hence by the observations of the previous lecture, \(a^{|\Z^*_m|}=1\) for every \(a\in \Z^*_m\). In the case that \(m\) is prime, this result is known as “Fermat’s Little Theorem” and is typically stated as \(a^{p-1}=1 \pmod{p}\) for every \(a\neq 0\).
One aspect that is often confusing in number-theoretic based cryptography, is that one needs to always keep track whether we are talking about “big” numbers or “small” numbers. In many cases in crypto, we use \(n\) to talk about our key size or security parameter, in which case we think of \(n\) as a “small” number of size \(100-1000\) or so. However, when we work with \(\Z^*_m\) we often think of \(m\) as a “big” number having about \(100-1000\) digits; that is \(m\) would be roughly \(2^{100}\) to \(2^{1000}\) or so. I will try to reserve the notation \(n\) for “small” numbers but may sometimes forget to do so, and other descriptions of RSA etc.. often use \(n\) for “big” numbers. It is important that whenever you see a number \(x\), you make sure you have a sense whether it is a “small” number (in which case \(poly(x)\) time is considered efficient) or whether it is a “large” number (in which case only \(poly(log(x))\) time would be considered efficient).
In much of this course we use \(m\) to denote a string which is our plaintext message to be encrypted or authenticated. In the context of integer factoring, it is convenient to use \(m=pq\) as the composite number that is to be factored. To keep things interesting (or more honestly, because I keep running out of letters) in this lecture we will have both usages of \(m\) (though hopefully not in the same theorem or definition!). When we talk about factoring, RSA, and Rabin, then we will use \(m\) as the composite number, while in the context of the abstract trapdoor-permutation based encryption and signatures we will use \(m\) for the message. When you see an instance of \(m\), make sure you understand what is its usage.
Primaliy testing
One procedure we often need is to find a prime of \(n\) bits. The typical way people do it is by choosing a random \(n\)-bit number \(p\), and testing whether it is prime. We showed in the previous lecture that a random \(n\) bit number is prime with probability at least \(\Omega(1/n^2)\) (in fact the probability is \(\tfrac{1\pm o(1)}{\ln n}\) by the Prime Number Theorem). We now discuss how we can test for primality.
There is an \(poly(n)\)-time algorithm to test whether a given \(n\)-bit number is prime or composite.
Theorem 10.3 was first shown in 1970’s by Solovay, Strassen, Miller and Rabin via a probabilistic algorithm (that can make a mistake with probability exponentially small in the number of coins it uses), and in a 2002 breakthrough, Agrawal, Kayal, and Saxena gave a deterministic polynomial time algorithm for the same problem.
There is a probabilistic polynomial time algorithm \(A\) that on input a number \(m\), if \(m\) is prime \(A\) outputs YES with probability \(1\) and if \(A\) is not even a “pseudoprime” it outputs NO with probability at least \(1/2\). (The definition of “pseudo-prime” will be clarified in the proof below.)
The algorithm is very simple and is based on Fermat’s Little Theorem: on input \(m\), pick a random \(a\in \{2,\ldots,m-1\}\), and if \(gcd(a,m)\neq 1\) or \(a^{m-1} \neq 1 \pmod{m}\) return NO and otherwise return YES.
By Fermat’s little theorem, the algorithm will always return YES on a prime \(m\). We define a “pseudoprime” to be a non-prime number \(m\) such that \(a^{m-1}=1 \pmod{m}\) for all \(a\) such that \(gcd(a,m)=1\).
If \(n\) is not a pseudoprime then the set \(S = \{ a\in\Z^*_m : a^{m-1}=1 \}\) is a strict subset of \(\Z^*_m\). But it is easy to see that \(S\) is a group and hence \(|S|\) must divide \(|Z^*_n|\) and hence in particular it must be the case that \(|S| < |\Z^*_n|/2\) and so with probability at least \(1/2\) the algorithm will output NO.
Lemma 10.4 its own might not seem very meaningful since it’s not clear how many pseudoprimes are there. However, it turns out these pseudoprimes, also known as “Carmichael numbers”, are much less prevalent than the primes, specifically, there are about \(N/2^{-\Theta(\log N/\log\log N)}\) pseudoprimes between \(1\) and \(N\). If we choose a random number \(m \in [2^n]\) and output it if and only if the algorithm of Lemma 10.4 algorithm outputs YES (otherwise resampling), then the probability we make a mistake and output a pseudoprime is equal to the ratio of the set of pseudoprimes in \([2^n]\) to the set of primes in \([2^n]\). Since there are \(\Omega(2^n/n)\) primes in \([2^n]\), this ratio is \(\tfrac{n}{2^{-\Omega(n/\log n)}}\) which is a negligible quantity. Moreover, as mentioned above, there are better algorithms that succeed for all numbers.
In contrast to testing if a number is prime or composite, there is no known efficient algorithm to actually find the factorization of a composite number. The best known algorithms run in time roughly \(2^{\tilde{O}(n^{1/3})}\) where \(n\) is the number of bits.
Fields
If \(p\) is a prime then \(\Z_p\) is a field which means it is closed under addition and multiplication and has \(0\) and \(1\) elements. One property of a field is the following:
If \(f\) is a nonzero polynomial of degree \(d\) over \(\Z_p\) then there are at most \(d\) distinct inputs \(x\) such that \(f(x)=0\).
(If you’re curious why, you can see that the task of, given \(x_1,\ldots,x_{d+1}\) finding the coefficients for a polynomial vanishing on the \(x_i\)’s amounts to solving a linear system in \(d+1\) variables with \(d+1\) equations that are independent due to the non-singularity of the Vandermonde matrix.)
In particular every \(x \in \Z_p\) has at most two square roots (numbers \(s\) such that \(s^2 = x \mod p\)). In fact, just like over the reals, every \(x\in\Z_p\) either has no square roots or exactly two square roots of the form \(\pm s\).
We can efficiently find square roots modulo a prime. In fact, the following result is known:
There is a probabilistic \(poly(\log p,d)\) time algorithm to find the roots of a degree \(d\) polynomial over \(\Z_p\).
This is a special case of the problem of factoring polynomials over finite fields, shown in 1967 by Berlekamp and on which much other work has been done; see Chapter 20 in Shoup).
Chinese remainder theorem
Suppose that \(m=pq\) is a product of two primes. In this case \(Z^*_m\) does not contain all the numbers from \(1\) to \(m-1\). Indeed, all the numbers of the form \(p,2p,3p,\ldots,(q-1)p\) and \(q,2q,\ldots,(p-1)q\) will have non-trivial g.c.d. with \(m\). There are exactly \(q-1 + p-1\) such numbers (because \(p\) and \(q\) are prime all the numbers of the forms above are distinct). Hence \(|Z^*_m| = m-1 - (p-1) - (q-1) = pq - p - q +1 = (p-1)(q-1)\).
Note that \(|Z^*_m|=|\Z^*_p|\cdot |\Z^*_q|\). It turns out this is no accident:
If \(m=pq\) then there is an isomorphism \(\varphi:\Z^*_m \rightarrow \Z^*_p \times \Z^*_q\). That is, \(\varphi\) is one to one and onto and maps \(x\in\Z^*_m\) into a pair \((\varphi_1(x),\varphi_2(x)) \in \Z^*_p \times \Z^*_q\) such that for every \(x,y \in \Z^*_m\):
* \(\varphi_1(x+y) = \varphi_1(x)+\varphi_1(y) \pmod{p}\)
* \(\varphi_2(x+y) = \varphi_2(x)+\varphi_2(y) \pmod{q}\)
* \(\varphi_1(x\cdot y) = \varphi_1(x)\cdot \varphi_1(y) \pmod{p}\)
* \(\varphi_2(x\cdot y) = \varphi_2(x)\cdot \varphi_2(y) \pmod{q}\)
\(\varphi\) simply maps \(x\in \Z^*_m\) to the pair \((x \mod p, x \mod q)\). Verifying that it satisfies all desired properties is a good exercise. QED
In particular, for every polynomial \(f()\) and \(x\in \Z^*_m\), \(f(x)=0 \pmod{m}\) iff \(f(x)=0 \pmod{p}\) and \(f(x)=0 \pmod{q}\). Therefore finding the roots of a polynomial \(f()\) modulo a composite \(m\) is easy if you know \(m\)’s factorization. However, if you don’t know the factorization then this is hard. In particular, extracting square roots is as hard as finding out the factors:
Suppose and there is an efficient algorithm \(A\) such that for every \(m\in \N\) and \(a\in \Z^*_m\), \(A(m,a^2 \pmod {m})=b\) such that \(a^2 = b^2 \pmod{m}\). Then, there is an efficient algorithm to recover \(p,q\) from \(m\).
Suppose that there is such an algorithm \(A\). Using the CRT we can define \(f:\Z^*_p\times\Z^*_q \rightarrow \Z^*_p\times \Z^*_q\) as \(f(x,y)=\varphi(A(\varphi^{-1}(x^2,y^2)))\) for all \(x\in \Z^*_p\) and \(y\in\Z^*_q\). Now, for any \(x,y\) let \((x',y')=f(x,y)\). Since \(x^2 = x'^2 \pmod{p}\) and \(y^2 = y'^2 \pmod{q}\) we know that \(x' \in \{\pm x \}\) and \(y' \in \{ \pm y \}\). Since flipping signs doesn’t change the value of \((x',y')=f(x,y)\), by flipping one or both of the signs of \(x\) or \(y\) we can ensure that \(x'=x\) and \(y'=-y\). Hence \((x,y)-(x',y')=(0,2y)\). In other words, if \(c = \varphi^{-1}(x-x',y-y')\) then \(c= 0 \pmod{p}\) but \(c \neq 0 \pmod{q}\) which in particular means that the greatest common divisor of \(c\) and \(m\) is \(q\). So, by taking \(gcd(A(\varphi^{-1}(x,y)),m)\) we will find \(q\), from which we can find \(p=m/q\).
This almost works, but there is a question of how can we find \(\varphi^{-1}(x,y)\), given that we don’t know \(p\) and \(q\)? The crucial observation is that we don’t need to. We can simply pick a value \(a\) at random in \(\{1,\ldots,m\}\). With very high probability (namely \((p-1+q-1)/pq\)) \(a\) will be in \(\Z^*_m\), and so we can imagine this process as equivalent to the process of taking a random \(x\in\Z^*_p\), a random \(y\in \Z^*_q\) and then flipping the signs of \(x\) and \(y\) randomly and taking \(a=\varphi(x,y)\). By the arguments above with probability at least \(1/4\), it will hold that \(gcd(a-A(a^2),m)\) will equal \(q\).
Note that this argument generalizes to work even if the algorithm \(A\) is an average case algorithm that only succeeds in finding a square root for a significant fraction of the inputs. This observation is crucial for cryptographic applications.
The RSA and Rabin functions
We are now ready to describe the RSA and Rabin trapdoor functions:
Given a number \(m=pq\) and \(e\) such that \(gcd((p-1)(q-1),e)=1\), the RSA function w.r.t \(m\) and \(e\) is the map \(f_{m,e}:\Z^*_m\rightarrow\Z^*_m\) such that \(\ensuremath{\mathit{RSA}}_{m,e}(x) = x^e \pmod{m}\).
Given a number \(m=pq\), the Rabin function w.r.t. \(m\), is the map \(Rabin_m:\Z^*_m\rightarrow \Z^*_m\) such that \(Rabin_m(x)=x^2 \pmod{m}\).
Note that both maps can be computed in polynomial time. Using the Chinese Remainder Theorem and Theorem 10.6, we know that both functions can be inverted efficiently if we know the factorization.1
However Theorem 10.6 is a much too big of a Hammer to invert the RSA and Rabin functions, and there are direct and simple inversion algorithms (see homework exercises). By Theorem 10.8, inverting the Rabin function amounts to factoring \(m\). No such result is known for the RSA function, but there is no better algorithm known to attack it than proceeding via factorization of \(m\). The RSA function has the advantage that it is a permutation over \(\Z^*_m\):
\(\ensuremath{\mathit{RSA}}_{m,e}\) is one to one over \(\Z^*_m\).
Suppose that \(\ensuremath{\mathit{RSA}}_{m,e}(a)=\ensuremath{\mathit{RSA}}_{m,e}(a')\). By the CRT, it means that there is \((x,y) \neq (x',y') \in \Z^*_p \times \Z^*_q\) such that \(x^e = x'^e \pmod{p}\) and \(y^e = y'^e \pmod{q}\). But if that’s the case we get that \((xx'^{-1})^e = 1 \pmod{p}\) and \((yy'^{-1})^e = 1 \pmod{q}\). But this means that \(e\) has to be a multiple of the order of \(xx'^{-1}\) and \(yy'^{-1}\) (at least one of which is not \(1\) and hence has order \(>1\)). But since the order always divides the group size, this implies that \(e\) has to have non-trivial gcd with either \(|Z^*_p|\) or \(|\Z^*_q|\) and hence with \((p-1)(q-1)\).
The RSA trapdoor function is known also as “plain” or “textbook” RSA encryption. This is because initially Diffie and Hellman (and following them, RSA) thought of an encryption scheme as a deterministic procedure and so considered simply encrypting a message \(x\) by applying \(\ensuremath{\mathit{ESA}}_{m,e}(x)\). Today however we know that it is insecure to use a trapdoor function directly as an encryption scheme without adding some randomization.
Abstraction: trapdoor permutations
We can abstract away the particular construction of the RSA and Rabin functions to talk about a general trapdoor permutation family. We make the following definition
A trapdoor permutation family (TDP) is a family of functions \(\{ p_k \}\) such that for every \(k\in\{0,1\}^n\), the function \(p_k\) is a permutation on \(\{0,1\}^n\) and:
* There is a key generation algorithm \(G\) such that on input \(1^n\) it outputs a pair \((k,\tau)\) such that the maps \(k,x \mapsto p_k(x)\) and \(\tau,y \mapsto p_k^{-1}(y)\) are efficiently computable.
- For every efficient adversary \(A\), \(\Pr_{(k,\tau) \leftarrow_R G(1^n), y\in\{0,1\}^n}[ A(k,y)=p_k^{-1}(y) ] < negl(n)\).
The RSA function is not a permutation over the set of strings but rather over \(\Z^*_m\) for some \(m=pq\). However, if we find primes \(p,q\) in the interval \([2^{n/2}(1-negl(n)),2^{n/2}]\), then \(m\) will be in the interval \([2^n(1-negl(n)),2^n]\) and hence \(\Z^*_m\) (which has size \(pq - p - q +1 = 2^n(1-negl(n))\)) can be thought of as essentially identical to \(\{0,1\}^n\), since we will always pick elements from \(\{0,1\}^n\) at random and hence they will be in \(\Z^*_m\) with probability \(1-negl(n)\). It is widely believed that for every sufficiently large \(n\) there is a prime in the interval \([2^n-poly(n),2^n]\) (this follows from the Extended Reimann Hypothesis) and Baker, Harman and Pintz proved that there is a prime in the interval \([2^n-2^{0.6n},2^n]\).2
Public key encryption from trapdoor permutations
Here is how we can get a public key encryption from a trapdoor permutation scheme \(\{ p_k \}\).
TDP-based public key encryption (TDPENC):
Key generation: Run the key generation algorithm of the TDP to get \((k,\tau)\). \(k\) is the public encryption key and \(\tau\) is the secret decryption key.
Encryption: To encrypt a message \(m\) with key \(k\in\{0,1\}^n\), choose \(x\in\{0,1\}^n\) and output \((p_k(x),H(x)\oplus m)\) where \(H:\{0,1\}^n\rightarrow\{0,1\}^\ell\) is a hash function we model as a random oracle.
Decryption: To decrypt the ciphertext \((y,z)\) with key \(\tau\), output \(m=H(p_k^{-1}(y))\oplus z\).
Please verify that you understand why TDPENC is a valid encryption scheme, in the sense that decryption of an encryption of \(m\) yields \(m\).
If \(\{ p_k \}\) is a secure TDP and \(H\) is a random oracle then TDPENC is a CPA secure public key encryption scheme.
Suppose, towards the sake of contradiction, that there is a polynomial-size adversary \(A\) that succeeds in the CPA game of TDPENC (with access to a random oracle \(H\)) with non-negligible advantage \(\epsilon\) over half. We will use \(A\) to design an algorithm \(I\) that inverts the trapdoor permutation.
Recall that the CPA game works as follows:
The adversary \(A\) gets as input a key \(k \in \{0,1\}^n\).
The algorithm \(A\) makes some polynomial amount of computation and \(T_1=poly(n)\) queries to the random oracle \(H\) and produces a pair of messages \(m_0,m_1 \in \{0,1\}^\ell\).
The “challenger” chooses \(b^* \leftarrow_R \{0,1\}\), chooses \(x^* \leftarrow_R \{0,1\}^n\) and computes the ciphertext \((y^*=p_k(x^*),z^* = H(x^*) \oplus m_{b^*})\) which is an encryption of \(m_{b^*}\).
The adversary \(A\) gets \((y^*,z^*)\) as input, makes some additional polynomial amount of computation and \(T_2=poly(n)\) queries to \(H\), and then outputs \(b\).
The adversary wins if \(b=b^*\).
We make the following claim:
CLAIM: With probability at least \(\epsilon\), the adversary \(A\) will make the query \(x^*\) to the random oracle.
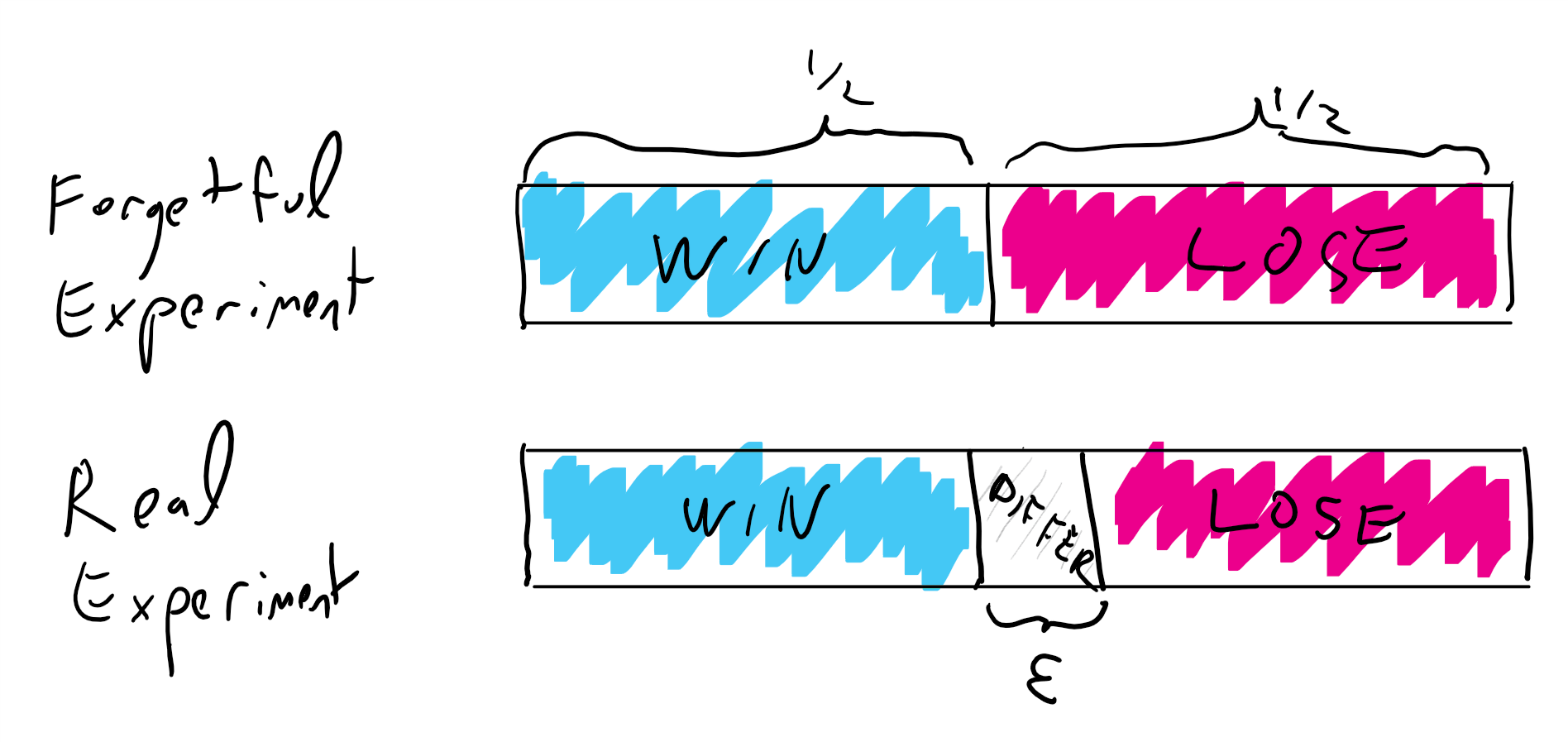
PROOF: Suppose otherwise. We will prove the claim using the “forgetful gnome” technique as used in the Boneh Shoup book. By the “lazy evaluation” paradigm, we can imagine that queries to \(H\) are answered by a “faithful gnome” that whenever presented with a new query \(x\), chooses a uniform and independent value \(w \leftarrow_R \{0,1\}^\ell\) as a response, and then records that \(H(x)=w\) to use that as answers for future queries.
Now consider the experiment where in the challenge part we use a “forgetful gnome” that answers \(H(x^*)\) by a uniform and independent string \(w^* \leftarrow_R \{0,1\}^\ell\) and does not record the answer for future queries. In the “forgetful experiment”, the second component of the ciphertext \(z^* = w^* \oplus m_{b^*}\) is distributed uniformly in \(\{0,1\}^\ell\) and independently from all other random choices, regardless of whether \(b^*=0\) or \(b^*=1\). Hence in this “forgetful experiment” the adversary gets no information about \(b^*\) and its probability of winning is at most \(1/2\). But the forgetful experiment is identical to the actual experiment if the value \(x^*\) is only queried to \(H\) once. Apart from the query of \(x^*\) by the challenger, all other queries to \(H\) are made by the adversary. Under our assumption, the adversary makes the query \(x^*\) with probability at most \(\epsilon\), and conditioned on this not happening the two experiments are identical. Since the probability of winning in the forgetful experiment is at most \(1/2\), the probability of winning in the overall experiment is less than \(1/2+\epsilon\), thus yielding a contradiction and establishing the claim. (These kind of analyses on sample spaces can be confusing; See Figure 10.1 for a graphical illustration of this argument.)
Given the claim, we can now construct our inverter algorithm \(I\) as follows:
The input to \(I\) is the key \(k\) to the trapdoor permutation and \(y^* = p_k(x^*)\). The goal of \(I\) is to output \(x^*\).
The inverter simulates the adversary in a CPA attack, answering all its queries to the oracle \(H\) by random values if they are new or the previously supplied answers if they were asked before. Whenever the adversary makes a query \(x\) to \(H\), \(I\) checks if \(p_h(x)=y^*\) and if so halts and outputs \(x\).
When the time comes to produce the challenge, the inverter \(I\) chooses \(z^*\) at random and provides the adversary with \((y^*,z^*)\) where \(z^* = w^* \oplus m_{b^*}\).3
The inverter continues the simulation again halting an outputting \(x\) if the adversary makes the query \(x\) such that \(p_k(x)=y^*\) to \(H\).
We claim that up to the point we halt, the experiment is identical to the actual attack. Indeed, since \(p_k\) is a permutation, we know that if the time came to produce the challenge and we have not halted, then the query \(x^*\) has not been made yet to \(H\). Therefore we are free to choose an independent random value \(w^*\) as the value \(H(x^*)\). (Our inverter does not know what the value \(x^*\) is, but this does not matter for this argument: can you see why?) Therefore, since by the claim the adversary will make the query \(x^*\) to \(H\) with probability at least \(\epsilon\), our inverter will succeed with the same probability.
This proof of Theorem 10.15 is not very long but it is somewhat subtle. Please re-read it and make sure you understand it. I also recommend you look at the version of the same proof in Boneh Shoup: Theorem 11.2 in Section 11.4 (“Encryption based on a trapdoor function scheme”).
We do not need to use a random oracle to get security in this scheme, especially if \(\ell\) is sufficiently short. We can replace \(H()\) with a hash function of specific properties known as a hard core construction; this was first shown by Goldreich and Levin.
Digital signatures from trapdoor permutations
Here is how we can get digital signatures from trapdoor permutations \(\{ p_k \}\). This is known as the “full domain hash” signatures.
Full domain hash signatures (FDHSIG):
Key generation: Run the key generation algorithm of the TDP to get \((k,\tau)\). \(k\) is the public verification key and \(\tau\) is the secret signing key.
Signing: To sign a message \(m\) with key \(\tau\), we output \(p_{k}^{-1}(H(m))\) where \(H:\{0,1\}^*\rightarrow\{0,1\}^n\) is a hash function modeled as a random oracle.
Verification: To verify a message-signature pair \((m,x)\) we check that \(p_k(x)=H(m)\).
We now prove the security of full domain hash:
If \(\{ p_k \}\) is a secure TDP and \(H\) is a random oracle then FDHSIG is chosen message attack secure digital signature scheme.
Suppose towards the sake of contradiction that there is a polynomial-sized adversary \(A\) that succeeds in a chosen message attack with non-negligible probability \(\epsilon>0\). We will construct an inverter \(I\) for the trapdoor permutation collection that succeeds with non-negligible probability as well.
Recall that in a chosen message attack the adversary makes \(T\) queries \(m_1,\ldots,m_T\) to its signing box which are interspersed with \(T'\) queries \(m'_1,\ldots,m'_{T'}\) to the random oracle \(H\). We can assume without loss of generality (by modifying the adversary and at most doubling the number of queries) that the adversary always queries the message \(m_i\) to the random oracle before it queries it to the signing box, though it can also make additional queries to the random oracle (and hence in particular \(T' \geq T\)). At the end of the attack the adversary outputs with probability \(\epsilon\) a pair \((x^*,m^*)\) such that \(m^*\) was not queried to the signing box and \(p_k(x^*)=H(m^*)\).
Our inverter \(I\) works as follows:
Input: \(k\) and \(y^*=p_k(y^*)\). Goal is to output \(x^*\).
\(I\) will guess at random \(t^*\) which is the step in which the adversary will query to \(H\) the message \(m^*\) that it is eventually going to forge in. With probability \(1/T'\) the guess will be correct.
\(I\) simulates the execution of \(A\). Except for step \(t^*\), whenever \(A\) makes a new query \(m\) to the random oracle, \(I\) will choose a random \(x\leftarrow \{0,1\}^n\), compute \(y=p_k(x)\) and designate \(H(m)=y\). In step \(t^*\), when the adversary makes the query \(m^*\), the inverter \(I\) will return \(H(m^*)=y^*\). \(I\) will record the values \((x,y)\) and so in particular will always know \(p_k^{-1}(H(m))\) for every \(H(m) \neq y^*\) that it returned as answer from its oracle on query \(m\).
When \(A\) makes the query \(m\) to the signature box, then since \(m\) was queried before to \(H\), if \(m \neq m^*\) then \(I\) returns \(x=p_k^{-1}(H(m))\) using its records. If \(m=m^*\) then \(I\) halts and outputs “failure”.
At the end of the game, the adversary outputs \((m^*,x^*)\). If \(p_k(x^*)=y^*\) then \(I\) outputs \(x^*\).
We claim that, conditioned on the probability \(\geq \epsilon/T'\) event that the adversary is successful and the final message \(m^*\) is the one queried in step \(t^*\), we provide a perfect simulation of the actual game. Indeed, while in an actual game, the value \(y=H(m)\) will be chosen independently at random in \(\{0,1\}^n\), this is equivalent to choosing \(x \leftarrow_R \{0,1\}^n\) and letting \(y=p_k(x)\). After all, a permutation applied to the uniform distribution is uniform.
Therefore with probability at least \(\epsilon/T'\) the inverter \(I\) will output \(x^*\) such that \(p_k(x^*)=y^*\) hence succeeding in the inverter.
Once again, this proof is somewhat subtle. I recommend you also read the version of this proof in Section 13.4 of Boneh-Shoup.
There is another reason to use hash functions with signatures. By combining a collision-resistant hash function \(h:\{0,1\}^* \rightarrow \{0,1\}^\ell\) with a signature scheme \((S,V)\) for \(\ell\)-length messages, we can obtain a signature for arbitrary length messages by defining \(S'_s(m)=S_s(h(m))\) and \(V'_v(m,\sigma)=V_v(h(m),\sigma)\).
Hardcore bits and security without random oracles
The main problem with using trapdoor functions as the basis of public key encryption is twofold: > * The fact that \(f\) is a trapdoor function does not rule out the possibility of computing \(x\) from \(f(x)\) when \(x\) is of some special form. Recall that the security of a one-way function is given over a uniformly random input. Usually messages to be sent are not drawn from a uniform distribution, and it’s possible that for some certain values of \(x\) it is easy to invert \(f(x)\), and those values of \(x\) also happen to be commonly sent messages. > * The fact that \(f\) is a trapdoor function does not rule out the possiblity of easily computing some partial information about \(x\) from \(f(x)\). Suppose we wished to play poker over a channel of bits. If even the suit or color of a card can be revealed from the encryption of that card, then it doesn’t matter if the entire encryption cannot be inverted; being able to compute even a single bit of the plaintext makes the entire game invalid. The RSA and Rabin functions have not been successfully reversed, but nobody has been able to prove that they give semantic security. > The solution to these issues is to use a hardcore predicate of a one-way function \(f\). We first define the security of a hardcore predicate, then show how it can be used to construct semantically secure encryption.
Let \(f:\{0, 1\}^n \rightarrow \{0, 1\}^n\) be a one-way function (we assume \(f\) is length preserving for simplicity), \(\ell(n)\) be a length function, and \(h: \{0, 1\}^n \rightarrow \{0, 1\}^{\ell(n)}\) be polynomial time computable. We say \(h\) is a hardcore predicate of \(f\) if for every efficient adversary \(A\), every polynomial \(p\), and all sufficiently large \(n\),
That is, given an input \(x \leftarrow_R \{0, 1\}^n\) chosen uniformly at random, no efficient adversary can distingusih between a random string \(r\) and \(b(x)\) given \(f(x)\) with non negligible advantage. This allows us to construct semantically secure public key encryption:
Hardcore predicate-based public key encryption:
Key generation: Run the standard key generation algorithm for the one-way function \(f\) to get \((e, d)\), where \(e\) is a public key used to compute the function \(f\) and \(d\) is a corresponding secret trapdoor key that makes it easy to invert \(f\).
Encryption: To encrypt a message \(m\) of length \(n\) with public key \(e\), pick \(x \leftarrow_R \{0, 1\}^n\) uniformly at random and compute \((f_e(x), b(x) \oplus m)\).
- Decryption: To decrypt the ciphertext \((c, c')\) we first use the secret trapdoor key \(d\) to compute \(D_d(c) = D_d(f_e(x)) = x\), then compute \(b(x)\) and \(b(x) \oplus c' = m\)
Please stop to verify that this is a valid public key encryption scheme.
Note that in this construction of public key encryption, the input to \(f\) is \(x\) drawn uniformly at random from \(\{0, 1\}^n\), so the defininition of the one-wayness of \(f\) can be applied directly. Furthermore, since \(b(x)\) is indistinguishable from a random string \(r\) even given \(f(x)\), the output \(b(x) \oplus m\) is essentially a one-time pad encryption of \(m\), where the key can only be retrieved by someone who can invert \(f\). Proving the security formally is left as an exercise.
This is all fine and good, but how do we actually construct a hardcore predicate? Blum and Micali were the first to construct a hardcore predicate based on the discrete logarithm problem, but the first construction for general one-way functions was given by Goldreich and Levin. Their idea is that if \(f\) is one-way, then it’s hard to guess the exclusive or of a random subset of the input to \(f\) when given \(f(x)\) and the subset itself.
Let \(f\) be a one-way function, and let \(g\) be defined as \(g(x, r) = (f(x), r)\), where \(|x| = |r|\). Let \(b(x, r) = \oplus_{i \in [n]} x_ir_i\) be the inner product \(\mod 2\) of \(x\) and \(r\). Then \(b\) is a hard core predicate of the function \(g\).
The proof of this theorem follows the classic proof by reduction method, where we assume the existence of an adversary that can predict \(b(x, r)\) given \(g(x, r)\) with non negligible advantage and construct an adversary that inverts \(f\) with non negligible probability. Let \(A\) be a (possibly randomized) program and \(\epsilon_A(n) > \tfrac{1}{p(n)}\) for some polynomial \(n\) such that
Where \(X_n\) and \(R_n\) are uniform and independent distributions over \(\{0, 1\}^n\). We observe that \(b\) being insecure and having an output of a single bit implies that such a program \(A\) exists. First, we show that on at least \(\epsilon_A(n)\) fraction of the possible inputs, program \(A\) has a \(\tfrac{\epsilon_A(n)}{2}\) advantage in predicting the output of \(b\).
There exists a set \(S \subseteq \{0, 1\}^n\) where \(|S| > \epsilon_A(n) (2^n)\) such that for all \(x \in S\),
The result follows from an averaging argument. Let \(k = \frac{|S|}{2^n}\), \(\displaystyle \alpha = \frac{1}{k} \sum_{x \in S} s(x)\) and \(\displaystyle \beta = \frac{1}{1 - k} \sum_{x \notin S} s(x)\) be the averages of \(s(x)\) over values in and not in \(S\), respectively, so \(k \alpha + (1 - k) \beta = \frac{1}{2} + \epsilon\). For notational convenience we set \(\epsilon = \epsilon_A(n)\). By definition \(\mathbb{E}[s(X_n)] = \frac{1}{2} + \epsilon\), so the fact that \(\alpha \leq 1\) and \(\beta < \frac{1}{2} + \frac{\epsilon}{2}\) gives \(k + (1 - k) \left( \frac{1}{2} + \frac{\epsilon}{2} \right) > \frac{1}{2} + \epsilon\), and solving finds that \(k > \epsilon\).
Now we observe that for any \(r \in \{0, 1\}^n\), we have
where \(e_i\) is the vector with all \(0\)s except a \(1\) in the \(i\)th location. This observation follows from the definition of \(b\), and it motivates the main idea of the reduction: Guess \(b(x, r)\) and use \(A\) to compute \(b(x, r \oplus e_i)\), then put it together to find \(x_i\) for all \(i\). The reason guessing works will become clear later, but intuitively the reason we cannot simply use \(A\) to compute both \(b(x, r)\) and \(b(x, r \oplus e_i)\) is that the probability \(A\) guesses both correctly is only (standard union) bounded below by \(1 - 2 \left( \tfrac{1}{2} - \epsilon_A(n)\right) = 2\epsilon_A(n)\). However, if we can guess \(b(x, r)\) correctly, then we only need to invoke \(A\) one time to get a better than half probability of correctly determining \(x_i\). It is then a simple matter of taking a majority vote over several such \(r\) to determine each \(x_i\).
Now the natural question is how can we possibly guess (and here we literally mean randomly guess) each value of \(b(x, r)\)? The key is that the values of \(r\) only need to be pairwise independent, since down the line we plan to use Chebyshev’s inequality on the accuracy of our guesses4. This means that while we need \(poly(n)\) many values of \(r\), we can get away with guessing \(\log (n)\) values of \(b(x, r)\) and combining them with some trickery to get more while preserving pairwise independence. Since \(2^{-\log n} = \tfrac{1}{n}\), with non negligible probability we can correctly guess all of our \(b(x, r)\) for polynomially many \(r\). We then use \(A\) to compute \(b(x, r \oplus e_i)\) for all \(r\) and \(i\), and since \(A\) has a non negligible advantage by majority vote we can retrieve each value of \(x_i\) to invert \(f\), thus contradicting the one-wayness of \(f\).
It is important that you understand why we cannot rely on invoking \(A\) twice, on both \(b(x, r)\) and \(b(x, r \oplus e_i)\). It is also important that you understand why, with non neligible probability, we can correctly guess \(b(x, r_1), \dots b(x, r_\ell)\) for \(r_1, \dots r_\ell\) chosen independently and uniformly at random and \(\ell = O(\log n)\). At the moment, it is not important what trickery is used to combine our guesses, but it will reduce confusion down the line if you understand why we can get away with pairwise independence in our inputs instead of complete mutual independence.
Before moving on to the formal proof of our theorem, please stop to convince yourself that, given that some trickery exists, this strategy works for inverting \(f\).
We use the assumed existence of \(A\) to construct \(B\), a program that inverts \(f\) (which we assume is length preserving for notational convenience). Pick \(n = |x|\) and \(l = \lceil \log(2n \cdot p(n)^2 + 1) \rceil\), where \(\epsilon_A(n) > \tfrac{1}{p(n)}\). Next, choose \(s^1, \dots s^l \in \{0, 1\}^n\) and \(\sigma^1, \dots \sigma^l \in \{0, 1\}\) all independently and uniformly at random. Here we set \(\sigma^i\) to be the guess for the value of \(b(x, s^i)\). For each non-empty subset \(J\) of \(\{1, 2, \dots l\}\) let \(r^J = \oplus_{j \in J} s^j\). We can observe that
by the properties of addition modulo 2, so we can say \(\rho^J = \oplus_{j \in J} \sigma^j\) is the correct guess for \(b(x, r^J)\) as long as each of \(\sigma^j\) for \(j \in J\) are correct. We can easily verify that the values \(r^J\) are pairwise independent and uniform, so this construction gives us \(poly(n)\) many correct pairs \((b(x, r^J), \rho^J)\) with probability \(\tfrac{1}{poly(n)}\), exactly as needed.
Define \(G(J, i) = \rho^J \oplus A(f(x), r^J \oplus e_i)\) to be the guess for \(x_i\) computed using input \(r^J\). From here, \(B\) simply needs to set \(x_i\) to the majority value of our guesses \(G(J, i)\) over the possible choices of \(J\) and output \(x\).
Now we prove that given that our guesses \(\rho^J\) are all correct, for all \(x \in S\) and for every \(1 \leq i \leq n\), we have
That is, with probability at least \(1 - O(\tfrac{1}{n})\), more than half of our \((2^l - 1)\) guesses for \(x_i\) are correct, where \(2^l - 1\) is the number of non empty subsets \(J\) of \(\{1, 2, \dots l\}\).
For every \(J\), define \(I_J\) to be the indicator that \(G(J, i) = x_i\), and we can observe that \(I_J\) is bernoulli with expected value \(s(x)\) (again, given that our guess for \(b(x, r^J)\) is correct). Pairwise independence of the \(I_J\) is given by the pairwise independence of the \(r^J\). Setting \(m = 2^l - 1\), defining \(s(x) = \tfrac{1}{2} + \tfrac{1}{q(n)}\), and using Chebyshev’s inequality, we get
Since \(x \in S\) we know \(\frac{1}{q(n)} \geq \frac{\epsilon_A(n)}{2} \geq \frac{1}{2p(n)}\), so
Putting it all together, \(B\) must first pick an \(x \in S\), then correctly guess \(\sigma^i\) for all \(i \in [1, 2, \dots l]\), then \(A\) must correctly compute \(b(x, r^J \oplus e_i)\) on more than half of the \(r^J\). Since each of these events happens independently, we get \(B\)’s success probability to be \(\epsilon_A(n) (\tfrac{1}{2^l})(1 - \tfrac{1}{2n}) = \epsilon_A(n) (\tfrac{1}{2n p(n)^2}) ( 1 - \tfrac{1}{2n}) > (\tfrac{1}{p(n)})(\tfrac{1}{2np(n)^2})(\tfrac{1}{2}) = \tfrac{1}{4n p(n)^3}\), which is non negligible in \(n\). This contradicts the assumption that \(f\) is a one way function, so no adversary \(A\) can predict \(b(x, r)\) given \((f(x), r)\) with a non negligible advantage, and \(b\) is a hardcore predicate of \(g\).
Extending to more than one hardcore bit
By definition, \(b\) as constructed above is only a hardcore predicate of length \(1\). While it’s great that this method works for any arbitrary one-way function, in the real world messages are sometimes longer than a single bit. Fortunately, there is hope: Goldreich and Levin’s hardcore bit construction can be used repeatedly to get a hardcore predicate of logarithmic length.
Let \(f\) be a one-way function, and define \(g_2(x, s) = (f(x), s)\), where \(|x| = n\) and \(|s| = 2n\). Let \(c > 0\) be a constant, and \(l(n) = \lceil c \log n \rceil\). Let \(b_i(x, s)\) denote the innter product mod 2 of the binary vectors \(x\) and \((s_{i + 1}, \dots s_{i + n})\), where \(s = (s_1, \dots s_{2n})\). Then the function \(h(x, s) = b_1(x, s) \dots b_{l(n)}(x, s)\) is a hardcore function of \(g_2\).
It’s clear that this is an imporant improvement on a single hardcore bit, but still nowhere near useable in general; imagine encrypting a text document with a key exponentially long in the size of the document. A completely different approach is needed to obtain a hardcore predicate with length polynomial in the key size. Bellare, Stepanovs, and Tessaro manage to pull it off using indistinguishability obfuscation of circuits, a cryptographic primitive which, like the existence of PRGs, is assumed to exist.
Let \(\mathbf{F}\) be a one-way function family and \(\mathbf{G}\) be a punctured PRF with the same input length of \(\mathbf{F}\). Then under the assumed existence of indistinguishability obfuscators, there exists a function family \(\mathbf{H}\) that is hardcore for \(\mathbf{F}\). Furthermore, the output length of \(\mathbf{H}\) is the same as the output length of \(\mathbf{G}\).
Since the output length of \(G\) can be polynomial in the length of its input, it follows that \(H\) outputs polynomially many hardcore bits in the length of its input. The proofs of Theorem 10.22 and Theorem 10.23 require the usage of results and concepts not yet covered in this course, but we refer interested readers to their original papers:
Goldreich, O., 1995. Three XOR-lemmas-an exposition. In Electronic Colloquium on Computational Complexity (ECCC).
Bellare, M., Stepanovs, I. and Tessaro, S., 2014, December. Poly-many hardcore bits for any one-way function and a framework for differing-inputs obfuscation. In International Conference on the Theory and Application of Cryptology and Information Security (pp. 102-121). Springer, Berlin, Heidelberg.
- ↩
Using Theorem 10.6 to invert the function requires \(e\) to be not too large. However, as we will see below it turns out that using the factorization we can invert the RSA function for every \(e\). Also, in practice people often use a small value for \(e\) (sometimes as small as \(e=3\)) for reasons of efficiency.
- ↩
Another, more minor issue is that the description of the key might not have the same length as \(\log m\); I defined them to be the same for simplicity of notation, and this can be ensured via some padding and concatenation tricks.
- ↩
It would have been equivalent to answer the adversary with a uniformly chosen \(z^*\) in \(\{0,1\}^\ell\), can you see why?
- ↩
This has to do with the fact that Chebyshev’s inequality is based on the variances of random variables. If we had to use the Chernoff bound we would be in trouble, since that requires full independence. For more on these and other concentration bounds, we recommend referring to the text Probability and Computing, by Eli Upfal.
Comments
Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.
Compiled on 11/17/2021 22:36:27
Copyright 2021, Boaz Barak.

This work is
licensed under a Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Produced using pandoc and panflute with templates derived from gitbook and bookdown.