Quantum computing and cryptography II

Bell’s Inequality is powerful demonstration that there is something very strange going on with quantum mechanics. But could this “strangeness” be of any use to solve computational problems not directly related to quantum systems? A priori, one could guess the answer is no. In 1994 Peter Shor showed that one would be wrong:

This is an exponential improvement over the best known classical algorithms, which as we mentioned before, take roughly \(2^{\tilde{O(\log^{1/3}m)}}\) time.

We will now sketch the ideas behind Shor’s algorithm. In fact, Shor proved the following more general theorem:

Recall that the order of \(g\) in \(\mathbb{G}\) is the smallest positive integer \(a\) such that \(g^a = 1\). By “given a group” we mean that we can represent the elements of the group as strings of length \(O(\log |\mathbb{G}|)\) and there is a \(poly(\log|\mathbb{G}|)\) algorithm to perform multiplication in the group.

From order finding to factoring and discrete log

The order finding problem allows not just to factor integers in polynomial time, but also solve the discrete logarithm over arbitrary Abelian groups, hereby showing that quantum computers will break not just RSA but also Diffie Hellman and Elliptic Curve Cryptography. We merely sketch how one reduces the factoring and discrete logarithm problems to order finding: (see some of the sources above for the full details)

• For factoring, let us restrict to the case \(m=pq\) for distinct \(p,q\). Recall that we showed that finding the size \((p-1)(q-1)=m-p-q+1\) of the group \(\Z^*_m\) is sufficient to recover \(p\) and \(q\). One can show that if we pick a few random \(x\)’s in \(\Z^*_m\) and compute their order, the least common multiplier of these orders is likely to be the group size.

• For discrete log in a group \(\mathbb{G}\), if we get \(X=g^x\) and need to recover \(x\), we can compute the order of various elements of the form \(X^ag^b\). The order of such an element is a number \(c\) satisfying \(c(xa+b) = 0 \pmod{|\mathbb{G}|}\). Again, with a few random examples we will get a non trivial example (where \(c \neq 0 \pmod{|\mathbb{G}|}\) ) and be able to recover the unknown \(x\).

Finding periods of a function: Simon’s Algorithm

Let \(\mathbb{H}\) be some Abelian group with a group operation that we’ll denote by \(\oplus\), and \(f\) be some function mapping \(\mathbb{H}\) to an arbitrary set (which we can encode as \(\{0,1\}^*\)). We say that \(f\) has period \(h^*\) for some \(h^*\in\mathbb{H}\) if for every \(x,y \in \mathbb{H}\), \(f(x)=f(y)\) if and only if \(y = x \oplus kh^*\) for some integer \(k\). Note that if \(\mathbb{G}\) is some Abelian group, then if we define \(\mathbb{H}=\Z_{|\mathbb{G}|}\), for every element \(g\in \mathbb{G}\), the map \(f(a)=g^a\) is a periodic map over \(\mathbb{H}\) with period the order of \(g\). So, finding the order of an item reduces to the question of finding the period of a function.

How do we generally find the period of a function? Let us consider the simplest case, where \(f\) is a function from \(\R\) to \(\R\) that is \(h^*\) periodic for some number \(h^*\), in the sense that \(f\) repeats itself on the intervals \([0,h^*]\), \([h^*,2h^*]\), \([2h^*,3h^*]\), etc.. How do we find this number \(h^*\)? The key idea would be to transform \(f\) from the time to the frequency domain. That is, we use the Fourier transform to represent \(f\) as a sum of wave functions. In this representation wavelengths that divide the period \(h^*\) would get significant mass, while wavelengths that don’t would likely “cancel out”.

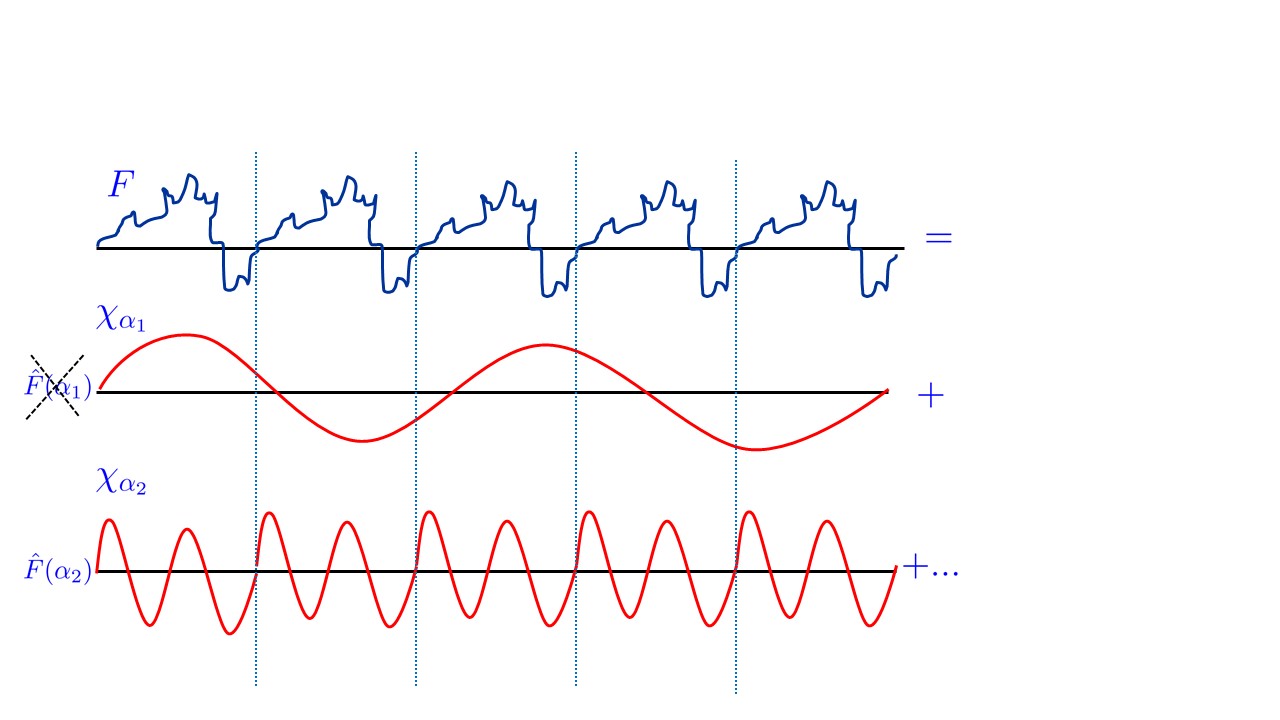
Similarly, the main idea behind Shor’s algorithm is to use a tool known as the quantum fourier transform that given a circuit computing the function \(f:\mathbb{H}\rightarrow\R\), creates a quantum state over roughly \(\log |\mathbb{H}|\) qubits (and hence dimension \(|\mathbb{H}|\)) that corresponds to the Fourier transform of \(f\). Hence when we measure this state, we get a group element \(h\) with probability proportional to the square of the corresponding Fourier coefficient. One can show that if \(f\) is \(h^*\)-periodic then we can recover \(h^*\) from this distribution.

Shor carried out this approach for the group \(\mathbb{H}=\Z^*_q\) for some \(q\), but we will start be seeing this for the group \(\mathbb{H} = \{0,1\}^n\) with the XOR operation. This case is known as Simon’s algorithm (given by Dan Simon in 1994) and actually preceded (and inspired) Shor’s algorithm:

Note that given \(O(n)\) such samples, we can recover \(h^*\) with high probability by solving the corresponding linear equations.

Simon’s algorithm seems to really use the special bit-wise structure of the group \(\{0,1\}^n\), so one could wonder if it has any relevance for the group \(\Z^*_m\) for some exponentially large \(m\). It turns out that the same insights that underlie the well known Fast Fourier Transform (FFT) algorithm can be used to essentially follow the same strategy for this group as well.

From Simon to Shor

(Note: The presentation here is adapted from the quantum computing chapter in my textbook with Arora.)

We now describe how to achieve Shor’s algorithm for order finding. We will not do this for a general group but rather focus our attention on the group \(\Z^*_{\ell}\) for some number \(\ell\) which is the case of interest for integer factoring and the discrete logarithm modulo primes problems.

That is, we prove the following theorem:

The idea is similar to Simon’s algorithm. We consider the map \(x \mapsto a^x (\mod \ell)\) which is a periodic map over \(\Z_m\) where \(m=|\Z^*_\ell|\) with period being the order of \(a\).
To find the period of this map we will now need to perform a Quantum Fourier Transform (QFT) over the group \(\Z_m\) instead of \(\{0,1\}^n\). This is a quantum algorithm that takes a register from some arbitrary state \(f \in \mathbb{C}^{m}\) into a state whose vector is the Fourier transform \(\hat{f}\) of \(f\). The QFT takes only \(O(\log^2 m)\) elementary steps and is thus very efficient. Note that we cannot say that this algorithm “computes” the Fourier transform, since the transform is stored in the amplitudes of the state, and as mentioned earlier, quantum mechanics give no way to “read out” the amplitudes per se. The only way to get information from a quantum state is by measuring it, which yields a single basis state with probability that is related to its amplitude. This is hardly representative of the entire Fourier transform vector, but sometimes (as is the case in Shor’s algorithm) this is enough to get highly non-trivial information, which we do not know how to obtain using classical (non-quantum) computers.

The Fourier transform over \(\Z_m\)

We now define the Fourier transform over \(\Z_m\) (the group of integers in \(\{0,\ldots,m-1\}\) with addition modulo \(m\)). We give a definition that is specialized to the current context. For every vector \(f\in\mathbb{C}^m\), the Fourier transform of \(f\) is the vector \(\hat{f}\) where the \(x^{th}\) coordinate of \(\hat{f}\) is defined as¹

\(\hat{f}(x) = \tfrac{1}{\sqrt{m}}\sum_{y\in\Z_m} f(x)\omega^{xy}\)

where \(\omega = e^{2\pi i/m}\).

The Fourier transform is simply a representation of \(f\) in the Fourier basis \(\{ \chi_x \}_{x \in \Z_m}\), where \(\chi_x\) is the vector/function whose \(y^{th}\) coordinate is \(\tfrac{1}{\sqrt{m}\omega^{xy}}\). Now the inner product of any two vectors \(\chi_x,\chi_z\) in this basis is equal to

But if \(x=z\) then \(\omega^{(x-z)}=1\) and hence this sum is equal to \(1\). On the other hand, if \(x \neq z\), then this sum is equal to \(\tfrac{1}{m} \tfrac{1 -\omega^{(x-y)m}}{1-\omega^{x-y}}= \tfrac{1}{m}\tfrac{1-1}{1-\omega^{x-y}}=0\) using the formula for the sum of a geometric series. In other words, this is an orthonormal basis which means that the Fourier transform map \(f \mapsto \hat{f}\) is a unitary operation.

What is so special about the Fourier basis? For one thing, if we identify vectors in \(\mathbb{C}^m\) with functions mapping \(\Z_m\) to \(\mathbb{C}\), then it’s easy to see that every function \(\chi\) in the Fourier basis is a homomorphism from \(\Z_m\) to \(\mathbb{C}\) in the sense that \(\chi(y+z)= \chi(y)\chi(z)\) for every \(y,z \in \Z_m\). Also, every function \(\chi\) is periodic in the sense that there exists \(r\in \Z_m\) such that \(\chi(y+r)=\chi(z)\) for every \(y\in \Z_m\) (indeed if \(\chi(y) = \omega^{xy}\) then we can take \(r\) to be \(\ell/x\) where \(\ell\) is the least common multiple of \(x\) and \(m\)). Thus, intuitively, if a function \(f:\Z_m\rightarrow\mathbb{C}\) is itself periodic (or roughly periodic) then when representing \(f\) in the Fourier basis, the coefficients of basis vectors with periods agreeing with the period of \(f\) should be large, and so we might be able to discover \(f\)’s period from this representation. This does turn out to be the case, and is a crucial point in Shor’s algorithm.

Fast Fourier Transform.

Denote by \(\ensuremath{\mathit{FT}}_m\) the operation that maps every vector \(f\in\mathbb{C}^m\) to its Fourier transform \(\hat{f}\). The operation \(\ensuremath{\mathit{FT}}_m\) is represented by an \(m\times m\) matrix whose \((x,y)\)th entry is \(\omega^{xy}\). The trivial algorithm to compute it takes \(m^2\) operations. The famous Fast Fourier Transform (FFT) algorithm computes the Fourier transform in \(O(m\log m)\) operations. We now sketch the idea behind the FFT algorithm as the same idea is used in the quantum Fourier transform algorithm.

Note that

\(\hat{f}(x) = \tfrac{1}{\sqrt{m}}\sum_{y\in\Z_m} f(y)\omega^{xy} =\)

\(\tfrac{1}{\sqrt{m}}\sum_{y\in\Z_m,y \;even} f(y)\omega^{-2x(y/2)} + \omega^x\tfrac{1}{\sqrt{m}}\sum_{y\in\Z_m,y \;odd} f(y)\omega^{2x(y-1)/2} \;.\)

Now since \(\omega^2\) is an \(m/2\)th root of unity and \(\omega^{m/2}=-1\), letting \(W\) be the \(m/2 \times m/2\) diagonal matrix with diagonal entries \(\omega^0,\ldots,\omega^{m/2-1}\), we get that

\(\ensuremath{\mathit{FT}}_m(f)_{low} = \ensuremath{\mathit{FT}}_{m/2}(f_{even}) + W \ensuremath{\mathit{FT}}_{m/2}(f_{odd})\)

\(\ensuremath{\mathit{FT}}_m(f)_{high} = \ensuremath{\mathit{FT}}_{m/2}(f_{even}) - W \ensuremath{\mathit{FT}}_{m/2}(f_{odd})\)

where for an \(m\)-dimensional vector \(\vec{v}\), we denote by \(\vec{v}_{even}\) (resp. \(\vec{v}_{odd}\)) the \(m/2\)-dimensional vector obtained by restricting \(\vec{v}\) to the coordinates whose indices have least significant bit equal to \(0\) (resp. \(1\)) and by \(\vec{v}_{low}\) (resp. \(\vec{v}_{high}\)) the restriction of \(\vec{v}\) to coordinates with most significant bit \(0\) (resp. \(1\)).

The equations above are the crux of the divide-and-conquer idea of the FFT algorithm, since they allow to replace a size-\(m\) problem with two size-\(m/2\) subproblems, leading to a recursive time bound of the form \(T(m) = 2T(m/2) + O(m)\) which solves to \(T(m)=O(m\log m)\).

Quantum Fourier Transform over \(\Z_m\)

The quantum Fourier transform is an algorithm to change the state of a quantum register from \(f \in \mathbb{C}^m\) to its Fourier transform \(\hat{f}\).

The crux of the algorithm is the FFT equations, which allow the problem of computing \(\ensuremath{\mathit{FT}}_m\), the problem of size \(m\), to be split into two identical subproblems of size \(m/2\) involving computation of \(\ensuremath{\mathit{FT}}_{m/2}\), which can be carried out recursively using the same elementary operations. (Aside: Not every divide-and-conquer classical algorithm can be implemented as a fast quantum algorithm; we are really using the structure of the problem here.)

We now describe the algorithm and the state, neglecting normalizing factors.

1. initial state: \(f= \sum_{x\in\Z_m} f(x)|x\rangle\)

2. Recursively run \(\ensuremath{\mathit{FT}}_{m/2}\) on \(m-1\) most significant qubits (state: \((\ensuremath{\mathit{FT}}_{m/2}f_{even})|0\rangle + (\ensuremath{\mathit{FT}}_{m/2}f_{odd})|1\rangle\))

3. If LSB is \(1\) then compute \(W\) on \(m-1\) most significant qubits (see below). (state : \((\ensuremath{\mathit{FT}}_{m/2}f_{even})|0\rangle + (W \ensuremath{\mathit{FT}}_{m/2}f_{odd})|1\rangle\))

4. Apply Hadmard gate \(H\) to least significant qubit. (state: \((\ensuremath{\mathit{FT}}_{m/2}f_{even})(|0\rangle+|1\rangle)\) \(+\) \((W \ensuremath{\mathit{FT}}_{m/2}f_{odd})(|0\rangle-|1\rangle) =\) \((\ensuremath{\mathit{FT}}_{m/2}f_{even}+ W \ensuremath{\mathit{FT}}_{m/2}f_{odd})|0\rangle + (\ensuremath{\mathit{FT}}_{m/2}f_{even}-W \ensuremath{\mathit{FT}}_{m/2}f_{odd})|1\rangle\))

5. Move LSB to the most significant position. (state: \(|0\rangle(\ensuremath{\mathit{FT}}_{m/2}f_{even}+ W \ensuremath{\mathit{FT}}_{m/2}f_{odd}) + |1\rangle(\ensuremath{\mathit{FT}}_{m/2}f_{even}- W \ensuremath{\mathit{FT}}_{m/2}f_{odd}) = \hat{f}\))

The transformation \(W\) on \(m-1\) qubits can be defined by \(|x\rangle \mapsto \omega^x = \omega^{\sum_{i=0}^{m-2} 2^ix_i}\) (where \(x_i\) is the \(i^{th}\) qubit of \(x\)). It can be easily seen to be the result of applying for every \(i\in \{ 0,\ldots,m-2\}\) the following elementary operation on the \(i^{th}\) qubit of the register:

\(|0\rangle \mapsto |0\rangle\) and \(|1\rangle \mapsto \omega^{2^i}|1\rangle\).

The final state is equal to \(\hat{f}\) by the FFT equations (we leave this as an exercise)

Shor’s Order-Finding Algorithm.

We now present the central step in Shor’s factoring algorithm: a quantum polynomial-time algorithm to find the order of an integer \(a\) modulo an integer \(\ell\).

Let \(t=\ceil{5\log (A+N)}\). Our register will consist of \(t+polylog(N)\) qubits. Note that the function \(x \mapsto A^x \pmod{N}\) can be computed in \(polylog(N)\) time and so we will assume that we can compute the map \(|x\rangle|y\rangle \mapsto |x\rangle|y\oplus (A^x \pmod{N\rangle)}\) (where we identify a number \(X \in \{ 0,\ldots,N-1\}\) with its representation as a binary string of length \(\log N\)).² Now we describe the order-finding algorithm. It uses a tool of elementary number theory called continued fractions which allows us to approximate (using a classical algorithm) an arbitrary real number \(\alpha\) with a rational number \(p/q\) where there is a prescribed upper bound on \(q\) (see below)

We now describe the algorithm and the state, this time including normalizing factors.

1. Apply Fourier transform to the first \(m\) bits. (state: \(\tfrac{1}{\sqrt{m}}\sum_{x\in\Z_m}|x\rangle)|0^n\rangle\))

2. Compute the transformation \(|x\rangle|y\rangle \mapsto |x\rangle|y \oplus (A^x \pmod{N\rangle)}\). (state: \(\tfrac{1}{\sqrt{m}}\sum_{x\in\Z_m} |x\rangle|A^x \pmod{N\rangle}\))

3. Measure the second register to get a value \(y_0\). (state: \(\tfrac{1}{\sqrt{K}}\sum_{\ell=0}^{K-1}|x_0 + \ell r\rangle|y_0\rangle\) where \(x_0\) is the smallest number such that \(A^{x_0} = y_0 \pmod{N}\) and \(K= \floor{(m-1-x_0)/r}\).)

4. Apply the Fourier transform to the first register. (state: \(\tfrac{1}{\sqrt{m}\sqrt{K}} \left(\sum_{x\in\Z_n}\sum_{\ell=0}^{K-1} \omega^{(x_0+\ell r)x}|x\rangle \right) |y_0\rangle\))

In the analysis, it will suffice to show that this algorithm outputs the order \(r\) with probability at least \(\Omega(1/\log N)\) (we can always amplify the algorithm’s success by running it several times and taking the smallest output).

Analysis: the case that \(r|m\)

We start by analyzing the algorithm in the case that \(m = rc\) for some integer \(c\). Though very unrealistic (remember that \(m\) is a power of \(2\)!) this gives the intuition why Fourier transforms are useful for detecting periods.

Claim: In this case the value \(x\) measured will be equal to \(ac\) for a random \(a \in \{0,\ldots,r-1\}\).

The claim concludes the proof since it implies that \(x/m = a/r\) where \(a\) is random integer less than \(r\). Now for every \(r\), at least \(\Omega(r/\log r)\) of the numbers in \([r-1]\) are co-prime to \(r\). Indeed, the prime number theorem says that there at least this many primes in this interval, and since \(r\) has at most \(\log r\) prime factors, all but \(\log r\) of these primes are co-prime to \(r\). Thus, when the algorithm computes a rational approximation for \(x/m\), the denominator it will find will indeed be \(r\).

To prove the claim, we compute for every \(x \in \Z_m\) the absolute value of \(|x\rangle\)’s coefficient before the measurement. Up to some normalization factor this is

\(\left| \sum_{\ell=0}^{c-1} \omega^{(x_0+\ell r)x} \right| = \left| \omega^{x_0c'c} \right| \left| \sum_{\ell=0}^{c-1} \omega^{r\ell x} \right| = 1 \cdot \left| \sum_{\ell=0}^{c-1} \omega^{r\ell x} \right| \;.\)

If \(c\) does not divide \(x\) then \(\omega^r\) is a \(c^{th}\) root of unity, so \(\sum_{\ell=0}^{c-1} w^{r \ell x} =0\) by the formula for sums of geometric progressions. Thus, such a number \(x\) would be measured with zero probability. But if \(x = cj\) then \(\omega^{r\ell x} = w^{r c j \ell} = \omega^{Mj} = 1\), and hence the amplitudes of all such \(x\)’s are equal for all \(j \in \{0, 2, \ldots, r-1\}\).

The general case

In the general case, where \(r\) does not necessarily divide \(m\), we will not be able to show that the measured value \(x\) satisfies \(m | xr\). However, we will show that with \(\Omega(1/\log r)\) probability, (1) \(xr\) will be “almost divisible” by \(m\) in the sense that \(0 \leq xr \pmod{m} < r/10\) and (2) \(\floor{xr/m}\) is coprime to \(r\).

Condition (1) implies that \(|xr - cM| < r/10\) for \(c=\floor{xr/m}\). Dividing by \(rM\) gives \(\left| \frac{x}{m} - \tfrac{c}{r} \right| < \tfrac{1}{10M}\). Therefore, \(\tfrac{c}{r}\) is a rational number with denominator at most \(N\) that approximates \(\frac{x}{m}\) to within \(1/(10M) < 1/(4N^4)\). It is not hard to see that such an approximation is unique (again left as an exercise) and hence in this case the algorithm will come up with \(c/r\) and output the denominator \(r\).

Thus all that is left is to prove the next two lemmas. The first shows that there are \(\Omega(r/\log r)\) values of \(x\) that satisfy the above two conditions and the second shows that each is measured with probability \(\Omega((1/\sqrt{r})^2) =\Omega(1/r)\).

Lemma 1: There exist \(\Omega(r/\log r)\) values \(x \in \Z_m\) such that:

1. \(0 < xr \pmod{m} < r/10\)

2. \(\floor{xr/m}\) and \(r\) are coprime

Lemma 2: If \(x\) satisfies \(0 < xr \pmod{m} < r/10\) then, before the measurement in the final step of the order-finding algorithm, the coefficient of \(|x\rangle\) is at least \(\Omega(\tfrac{1}{\sqrt{r}})\).

Proof of Lemma 1 We prove the lemma for the case that \(r\) is coprime to \(m\), leaving the general case to the reader. In this case, the map \(x \mapsto rx \pmod{m}\) is a permutation of \(\Z^*_m\). There are at least \(\Omega(r/\log r)\) numbers in \([1..r/10]\) that are coprime to \(r\) (take primes in this range that are not one of \(r\)’s at most \(\log r\) prime factors) and hence \(\Omega(r/\log r)\) numbers \(x\) such that \(rx \pmod{m} = xr - \floor{xr/m}m\) is in \([1..r/10]\) and coprime to \(r\). But this means that \(\floor{rx/m}\) can not have a nontrivial shared factor with \(r\), as otherwise this factor would be shared with \(rx \pmod{m}\) as well.

Proof of Lemma 2: Let \(x\) be such that \(0 < xr \pmod{m} < r/10\). The absolute value of \(|x\rangle\)’s coefficient in the state before the measurement is

where \(K = \floor{(m-x_0-1)/r}\). Note that \(\tfrac{m}{2r} < K < \tfrac{m}{r}\) since \(x_0 < N \ll m\).

Setting \(\beta=\omega^{rx}\) (note that since \(m \not| rx\), \(\beta \neq 1\)) and using the formula for the sum of a geometric series, this is at least \(\tfrac{\sqrt{r}}{2M}\left| \tfrac{1 - \beta^{\ceil{m/r}}}{1-\beta} \right| = \tfrac{\sqrt{r}}{2M}\tfrac{\sin(\theta\ceil{m/r}/2)}{\sin(\theta/2)} \;,\) where \(\theta=\tfrac{rx \pmod{m}}{m}\) is the angle such that \(\beta = e^{i\theta}\) (see Figure [quantum:fig:theta] for a proof by picture of the last equality). Under our assumptions \(\ceil{m/r}\theta<1/10\) and hence (using the fact that \(\sin \alpha \sim \alpha\) for small angles \(\alpha\)), the coefficient of \(x\) is at least \(\tfrac{\sqrt{r}}{4M}\ceil{m/r} \geq \tfrac{1}{8\sqrt{r}}\)

This completes the proof of Theorem 19.6.

Rational approximation of real numbers

In many settings, including Shor’s algorithm, we are given a real number in the form of a program that can compute its first \(t\) bits in \(poly(t)\) time. We are interested in finding a close approximation to this real number of the form \(a/b\), where there is a prescribed upper bound on \(b\). Continued fractions is a tool in number theory that is useful for this.

A continued fraction is a number of the following form: \(a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \tfrac{1}{a_3 + \ldots}} }\) for \(a_0\) a non-negative integer and \(a_1,a_2,\ldots\) positive integers.

Given a real number \(\alpha>0\), we can find its representation as an infinite fraction as follows: split \(\alpha\) into the integer part \(\floor{\alpha}\) and fractional part \(\alpha - \floor{\alpha}\), find recursively the representation \(R\) of \(1/(\alpha - \floor{\alpha})\), and then write

If we continue this process for \(n\) steps, we get a rational number, denoted by \([a_0,a_1,\ldots,a_n]\), which can be represented as \(\tfrac{p_n}{q_n}\) with \(p_n,q_n\) coprime. The following facts can be proven using induction:

• \(p_0=a_0, q_0 =1\) and for every \(n>1\), \(p_n = a_np_{n-1} + p_{n-2}\), \(q_n = a_nq_{n-1} + q_{n-2}\).

• \(\tfrac{p_n}{q_n} - \tfrac{p_{n-1}}{q_{n-1}} = \tfrac{(-1)^{n-1}}{q_nq_{n-1}}\)

Furthermore, it is known that \(\Bigl|\tfrac{p_n}{q_n} - \alpha\Bigl| < \tfrac{1}{q_nq_{n+1}} (*)\) which implies that \(\tfrac{p_n}{q_n}\) is the closest rational number to \(\alpha\) with denominator at most \(q_n\). It also means that if \(\alpha\) is extremely close to a rational number, say, \(\left|\alpha - \tfrac{a}{b} \right| < \tfrac{1}{4b^4}\) for some coprime \(a,b\) then we can find \(a,b\) by iterating the continued fraction algorithm for \(polylog(b)\) steps. Indeed, let \(q_n\) be the first denominator such that \(q_{n+1} \geq b\). If \(q_{n+1} > 2b^2\) then \((*)\) implies that \(\bigl|\tfrac{p_n}{q_n}-\alpha\bigr| < \tfrac{1}{2b^2}\). But this means that \(\tfrac{p_n}{q_n} = \tfrac{a}{b}\) since there is at most one rational number of denominator at most \(b\) that is so close to \(\alpha\). On the other hand, if \(q_{n+1} \leq 2b^2\) then since \(\tfrac{p_{n+1}}{q_{n+1}}\) is closer to \(\alpha\) than \(\tfrac{a}{b}\), \(\bigl|\tfrac{p_{n+1}}{q_{n+1}}-\alpha\bigr| < \tfrac{1}{4b^4}\;,\) again meaning that \(\tfrac{p_{n+1}}{q_{n+1}}=\tfrac{a}{b}\). It’s not hard to verify that \(q_n \geq 2^{n/2}\), implying that \(p_n\) and \(q_n\) can be computed in \(polylog(q_n)\) time.

Quantum cryptography

There is another way in which quantum mechanics interacts with cryptography. These “spooky actions at a distance” have been suggested by Weisner and Bennet-Brassard as a way in which parties can create a secret shared key over an insecure channel. On one hand, this concept does not require as much control as general-purpose quantum computing, and so it has in fact been demonstrated physically. On the other hand, unlike transmitting standard digital information, this “insecure channel” cannot be an arbitrary media such as wifi etc.. but rather one needs fiber optics, lasers, etc.. Unlike quantum computers, where we only need one of those to break RSA, to actually use key exchange at scale we need to setup these type of networks, and so it is unclear if this approach will ever dominate the solution of Alice sending to Bob a Brink’s truck with the shared secret key. People have proposed some other ways to use the interesting properties of quantum mechanics for cryptographic purposes including quantum money and quantum software protection.

Comments

Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.

Compiled on 11/17/2021 22:36:06

Copyright 2021, Boaz Barak.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Produced using pandoc and panflute with templates derived from gitbook and bookdown.