See any bugs/typos/confusing explanations? Open a GitHub issue. You can also comment below

★ See also the PDF version of this chapter (better formatting/references) ★

Pseudorandom functions

Reading: Rosulek Chapter 6 has a good description of pseudorandom functions. Katz-Lindell cover pseudorandom functions in a different order than us. The topics of this lecture and the next ones are covered in KL sections 3.4-3.5 (PRFs and CPA security), 4.1-4.3 (MACs), and 8.5 (construction of PRFs from PRG).

In the last lecture we saw the notion of pseudorandom generators, and introduced the PRG conjecture, which stated that there exists a pseudorandom generator mapping \(n\) bits to \(n+1\) bits. We have seen the length extension theorem, which states that given such a pseudorandom generator, there exists a generator mapping \(n\) bits to \(m\) bits for an arbitrarily large polynomial \(m(n)\). But can we extend it even further? Say, to \(2^n\) bits? Does this question even make sense? And why would we want to do that? This is the topic of this lecture.

At a first look, the notion of extending the output length of a pseudorandom generator to \(2^n\) bits seems nonsensical. After all, we want our generator to be efficient and just writing down the output will take exponential time. However, there is a way around this conundrum. While we can’t efficiently write down the full output, we can require that it would be possible, given an index \(i\in \{0,\ldots,2^n-1\}\), to compute the \(i^{th}\) bit of the output in polynomial time.1 That is, we require that the function \(i \mapsto G(s)_i\) is efficiently computable and (by security of the pseudorandom generator) indistinguishable from a function that maps each index \(i\) to an independent random bit in \(\{0,1\}\). This is the notion of a pseudorandom function generator which is a bit subtle to define and construct, but turns out to have a great many applications in cryptography.

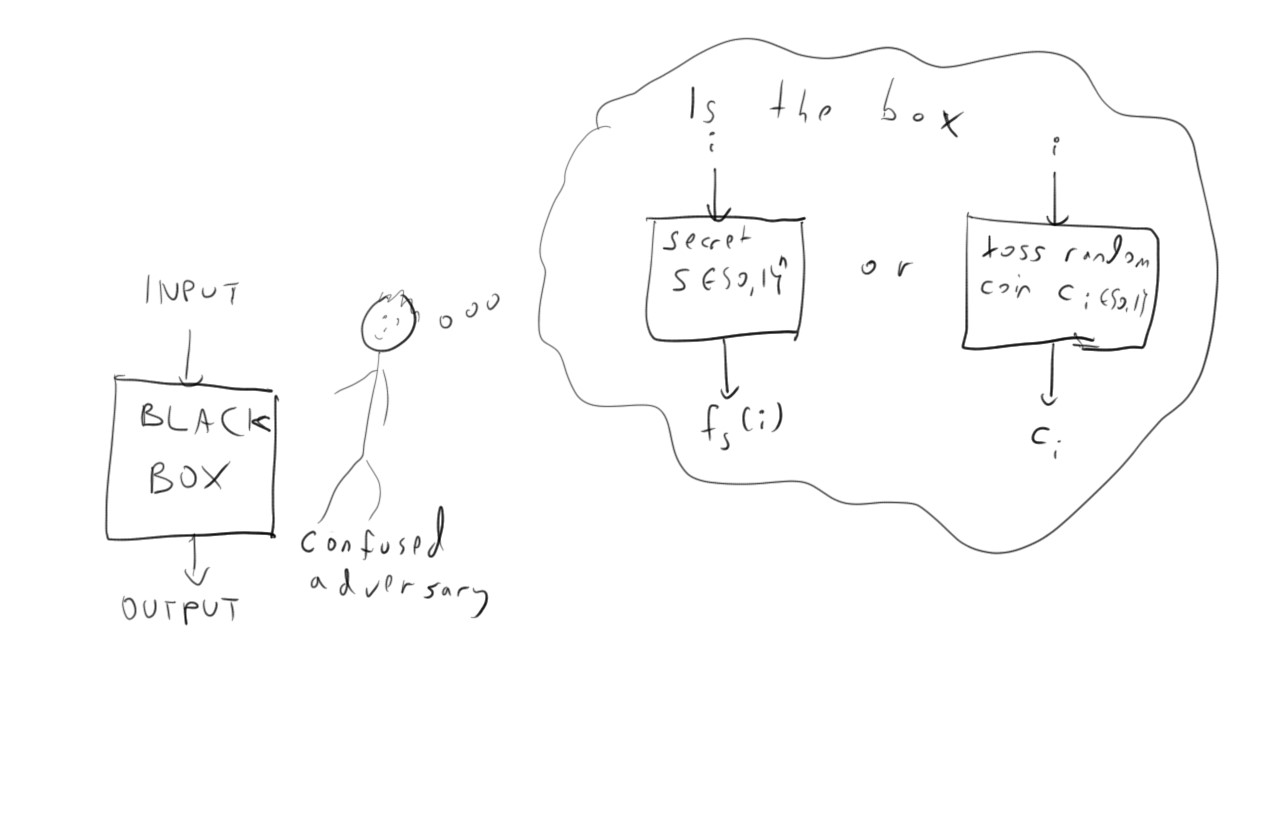
An efficiently computable function \(F\) taking two inputs \(s\in\{0,1\}^*\) and \(i \in \{0,\ldots,2^{|s|}-1\}\) and outputting a single bit \(F(s,i)\) is a pseudorandom function (PRF) generator if for every polynomial time adversary \(A\) outputting a single bit and polynomial \(p(n)\), if \(n\) is large enough then:

\[ \left| \E_{s\in\{0,1\}^n}[ A^{F(s,\cdot)}(1^n)] - \E_{H \leftarrow_R [2^n]\rightarrow\{0,1\}}[A^H(1^n)] \right| < 1/p(n) \;.\]

Some notes on notation are in order. The input \(1^n\) is simply a string of \(n\) ones, and it is a typical cryptography convention to assume that such an input is always given to the adversary. This is simply because by “polynomial time adversary” we really mean polynomial in \(n\) (which is our key size or security parameter)2. The notation \(A^{F(s,\cdot)}\) means that \(A\) has black box (also known as oracle) access to the function that maps \(i\) to \(F(s,i)\). That is, \(A\) can choose an index \(i\), query the box and get \(F(s,i)\), then choose a new index \(i'\), query the box to get \(F(s,i')\), and so on for a polynomial number of queries. The notation \(H \leftarrow_R [2^n] \rightarrow \{0,1\}\) means that \(H\) is a completely random function that maps every index \(i\) to an independent and random different bit.

This notion of a randomly chosen function can be difficult to wrap your mind around. Try to imagine a table of all of the strings in \(\{0, 1\}^n\). We now go to each possible input, randomly generate a bit to be its output, and write down the result in the table. When we’re done, we have a length \(2^n\) lookup table that maps each input to an output that was generated uniformly at random and independently of all other outputs. This lookup table is now our random function \(H\).

In practice it’s too cumbersome to actually generate all \(2^n\) bits, and sometimes in theory it’s convenient to think of each output as generated only after a query is made. This leads to adopting the lazy evaluation model. In the lazy evaluation model, we imagine that a lazy person is sitting in a room with the same lookup table as before, but with all entries blank. If someone makes some query \(H(s)\), the lazy person checks if the entry for \(s\) in the lookup table is blank. If so, the lazy evaluator generates a random bit, writes down the result for \(s\), and returns it. Otherwise, if an output has already been generated for \(s\) previously (because \(s\) has been queried before), the lazy evaluator simply returns this value. Can you see why this model is more convenient in some ways?

One last way to think about how a completely random function is determined is to first observe that there exist a total of \(2^{2^n}\) functions from \(\{0, 1\}^n\) to \(\{0, 1\}\) (can you see why? It may be easier to think of them as functions from \([2^n]\) to \(\{0, 1\}\)). We choose one of them uniformly at random to be \(H\), and it’s still the case that for any given input \(s\) the result \(H(s)\) is \(0\) or \(1\) with equal probability independent of any other input.

Regardless of which model we use to think about generating \(H\), after we’ve chosen \(H\) and put it in a black box, the behavior of \(H\) is in some sense “deterministic” because given the same query it will always return the same result. However, before we ever make any given query \(s\) we can only guess \(H(s)\) correctly with probability \(\tfrac{1}{2}\), because without previously observing \(H(s)\) it is effectively random and undecided to us (just like in the lazy evaluator model).

Now would be a fantastic time to stop and think deeply about the three constructions in the remark above, and in particular why they are all equivalent. If you don’t feel like thinking then at the very least you should make a mental note to come back later if you’re confused, because this idea will be very useful down the road.

Thus, the notation \(A^H\) in the PRF definition means \(A\) has access to a completely random black box that returns a random bit for any new query made, and on previously seen queries returns the same bit as before. Finally one last note: below we will identify the set \([2^n] = \{0,\ldots,2^n-1\}\) with the set \(\{0,1\}^n\) (there is a one to one mapping between those sets using the binary representation), and so we will treat \(i\) interchangeably as a number in \([2^n]\) or a string in \(\{0,1\}^n\).

Ensembles of PRFs. If \(F\) is a pseudorandom function generator, then if we choose a random string \(s\) and consider the function \(f_s\) defined by \(f_s(i) = F(s,i)\), no efficient algorithm can distinguish between black box access to \(f_s(\cdot)\) and black box access to a completely random function (see Figure 4.1). Notably, black box access implies that a priori the adversary does not know which function it’s querying. From the adversary’s point of view, they query some oracle \(O\) (which behind the scenes is either \(f_s(\cdot)\) or \(H\)), and must decide if \(O = f_s(\cdot)\) or \(O = H\). Thus often instead of talking about a pseudorandom function generator we will refer to a pseudorandom function ensemble \(\{ f_s \}_{s\in \{0,1\}^*}\). Formally, this is defined as follows:

Let \(\{ f_s \}_{s\in \{0,1\}^*}\) be an ensemble of functions such that for every \(s\in \{0,1\}^*\), \(f_s:\{0,1\}^{|s|} \rightarrow \{0,1\}\). We say that \(\{ f_s \}\) is a pseudorandom function ensemble if the function \(F\) that on input \(s\in \{0,1\}^*\) and \(i \in \{0,\ldots,2^{|s|}-1\}\) outputs \(f_s(i)\) is a PRF generator.

Note that the condition of Definition 4.3 corresponds to requiring that for every polynomial \(p\) and \(p(n)\)-time adversary \(A\), if \(n\) is large enough then

\[ \left| \E_{s\in\{0,1\}^n}[ A^{f_s(\cdot)}(1^n)] - \E_{h \leftarrow_R \mathcal{F}_{n,1} }[A^h(1^n)] \right| < 1/p(n)\]
where \(\mathcal{F}_{n,1}\) is the set of all functions mapping \(\{0,1\}^n\) to \(\{0,1\}\) (i.e., the set \(\{0,1\}^n \rightarrow \{0,1\}\)).

It is worth while to pause and make sure you understand why Definition 4.3 and Definition 4.1 give different ways to talk about the same object.

4.1: In a pseudorandom function, an adversary cannot tell whether they are given a black box that computes the function \(i \mapsto F(s,i)\) for some secret \(s\) that was chosen at random and fixed, or whether the black box computes a completely random function that tosses a fresh random coin whenever it’s given a new input \(i\).

In the next lecture we will see the proof of following theorem (due to Goldreich, Goldwasser, and Micali)

Assuming the PRG conjecture, there exists a secure pseudorandom function generator.

But before we see the proof of Theorem 4.4, let us see why pseudorandom functions could be useful.

One time passwords (e.g. Google Authenticator, RSA ID, etc.)

Until now we have talked about the task of encryption, or protecting the secrecy of messages. But the task of authentication, or protecting the integrity of messages is no less important. For example, consider the case that you receive a software update for your PC, phone, car, pacemaker, etc. over an open channel such as an unencrypted Wi-Fi connection. The contents of that update are not secret, but it is of crucial importance that it was unchanged from the message sent out by the company and that no malicious attacker had modified the code. Similarly, when you log into your bank, you might be much more concerned about the possibility of someone impersonating you and cleaning out your account than you are about the secrecy of your information.

Let’s start with a very simple scenario which we’ll call the login problem. Alice and Bob share a key as before, but now Alice wants to simply prove her identity to Bob. What makes this challenging is that this time they need to contend with not the passive eavesdropping Eve but the active adversary Mallory, who completely controls the communication channel between them and can modify (or mall) any message that they send. Specifically for the identity proving case, we think of the following scenario. Each instance of such an identification protocol consists of some interaction between Alice and Bob that ends with Bob deciding whether to accept it as authentic or reject as an impersonation attempt. Mallory’s goal is to fool Bob into accepting her as Alice.

The most basic way to try to solve the login problem is by simply using a password. That is, if we assume that Alice and Bob can share a key, we can treat this key as some secret password \(p\) that was selected at random from \(\{0,1\}^n\) (and hence can only be guessed with probability \(2^{-n}\)). Why doesn’t Alice simply send \(p\) to Bob to prove to him her identity? A moment’s thought shows that this would be a very bad idea. Since Mallory is controlling the communication line, she would learn \(p\) after the first identification attempt and could then easily impersonate Alice in future interactions. However, we seem to have just the tool to protect the secrecy of \(p\)— encryption. Suppose that Alice and Bob share a secret key \(k\) and an additional secret password \(p\). Wouldn’t a simple way to solve the login problem be for Alice to send Bob an encryption of the password \(p\)? After all, the security of the encryption should guarantee that Mallory can’t learn \(p\), right?

This would be a good time to stop reading and try to think for yourself whether using a secure encryption to encrypt \(p\) would guarantee security for the login problem. (No really, stop and think about it.)

The problem is that Mallory does not have to learn the password \(p\) in order to impersonate Alice. For example, she can simply record the message Alice \(c_1\) sends to Bob in the first session and then replay it to Bob in the next session. Since the message is a valid encryption of \(p\), then Bob would accept it from Mallory! (This is known as a replay attack and is a common attack one needs to protect against in cryptographic protocols.) One can try to put in countermeasures to defend against this particular attack, but its existence demonstrates that secrecy of the password does not guarantee security of the login protocol.

How do pseudorandom functions help in the login problem?

The idea is that they create what’s known as a one time password. Alice and Bob will share an index \(s\in\{0,1\}^n\) for the pseudorandom function generator \(\{ f_s \}\). When Alice wants to prove her identity to Bob, Bob will choose a random \(i\leftarrow_R\{0,1\}^n\), send \(i\) to Alice, and then Alice will send \(f_s(i),f_s(i+1),\ldots,f_s(i+\ell-1)\) to Bob where \(\ell\) is some parameter (you can think of \(\ell=n\) for simplicity). Bob will check that indeed \(y=f_s(i)\) and if so accept the session as authentic.

The formal protocol is as follows:

Protocol PRF-Login:

  • Shared input: \(s\in\{0,1\}^n\). Alice and Bob treat it as a seed for a pseudorandom function generator \(\{ f_s \}\).
  • In every session Alice and Bob do the following:
    1. Bob chooses a random \(i\leftarrow_R[2^n]\) and sends \(i\) to Alice.
    2. Alice sends \(y_1,\ldots,y_\ell\) to Bob where \(y_j = f_s(i+j-1)\).
    3. Bob checks that for every \(j\in\{1,\ldots,\ell\}\), \(y_j = f_s(i+j-1)\) and if so accepts the session; otherwise he rejects it.

As we will see it’s not really crucial that the input \(i\) (which is known in crypto parlance as a nonce) is random. What is crucial is that it never repeats itself, to foil a replay attack. For this reason in many applications Alice and Bob compute \(i\) as a function of the current time (for example, the index of the current minute based on some agreed-upon starting point), and hence we can make it into a one message protocol. Also the parameter \(\ell\) is sometimes chosen to be deliberately short so that it will be easy for people to type the values \(y_1,\ldots,y_\ell\).

12.1: The Google Authenticator app is one popular example of a one-time password scheme using pseudorandom functions. Another example is RSA’s SecurID token.

Why is this secure? The key to understanding schemes using pseudorandom functions is to imagine what would happen if \(f_s\) was be an actual random function instead of a pseudo random function. In a truly random function, every one of the values \(f_s(0),\ldots,f_s(2^n-1)\) is chosen independently and uniformly at random from \(\{0,1\}\). One useful way to imagine this is using the concept of “lazy evaluation”. We can think of \(f_S\) as determined by tossing \(2^n\) different coins for the values \(f(0),\ldots,f(2^n-1)\). Now consider the case where we don’t actually toss the \(i^{th}\) coin until we need it. The crucial point is that if we have queried the function in \(T\ll 2^n\) places, then when Bob chooses a random \(i\in[2^n]\) it is extremely unlikely that any one of the set \(\{i,i+1,\ldots,i+\ell-1\}\) will be one of those locations that we previously queried. Thus, if the function was truly random, Mallory has no information on the value of the function in these coordinates, and would be able to predict (or rather, guess) it in all these locations with probability at most \(2^{-\ell}\).

Please make sure you understand the informal reasoning above, since we will now translate this into a formal theorem and proof.

Suppose that \(\{ f_s \}\) is a secure pseudorandom function generator and Alice and Bob interact using Protocol PRF-Login for some polynomial number \(T\) of sessions (over a channel controlled by Mallory). After observing these interactions, Mallory then interacts with Bob, where Bob follows the protocol’s instructions but Mallory has access to arbitrary efficient computation. Then, the probability that Bob accepts the interaction is at most \(2^{-\ell}+\mu(n)\) where \(\mu(\cdot)\) is some negligible function.

This proof, as so many others in this course, uses an argument via contradiction. We assume, towards the sake of contradiction, that there exists an adversary \(M\) (for Mallory) that can break the identification scheme PRF-Login with probability \(2^{-\ell}+\epsilon\) after \(T\) interactions. We then construct an attacker \(A\) that can distinguish access to \(\{ f_s \}\) from access to a random function in \(poly(T)\) time and with bias at least \(\epsilon/2\).

How do we construct this adversary \(A\)? The idea is as follows. First, we prove that if we ran the protocol PRF-Login using an actual random function, then \(M\) would not be able to succeed in impersonating with probability better than \(2^{-\ell}+negligible\). Therefore, if \(M\) does do better, then we can use that to distinguish \(f_s\) from a random function. The adversary \(A\) gets some black box \(O(\cdot)\) (for oracle) and will use it while internally simulating all the parties— Alice, Bob and Mallory (using \(M\)) in the \(T+1\) interactions of the PRF-Login protocol. Whenever any of the parties needs to evaluate \(f_s(i)\), \(A\) will forward \(i\) to its black box \(O(\cdot)\) and return the value \(O(i)\). It will then output \(1\) if and only if \(M\) succeeds in impersonation in this internal simulation. The argument above showed that if \(O(\cdot)\) is a truly random function, then the probability that \(A\) outputs \(1\) is at most \(2^{-\ell}+negligible\) (and so in particular less than \(2^{-\ell}+\epsilon/2\)). On the other hand, if \(O(\cdot)\) is the function \(i \mapsto f_s(i)\) for some fixed and random \(s\), then this probability is at least \(2^{-\ell}+\epsilon\). Thus \(A\) will distinguish between the two cases with bias at least \(\epsilon/2\). We now turn to the formal proof:

Claim 1: Let PRF-Login* be the hypothetical variant of the protocol PRF-Login where Alice and Bob share a completely random function \(H:[2^n]\rightarrow\{0,1\}\). Then, no matter what Mallory does, the probability she can impersonate Alice after observing \(T\) interactions is at most \(2^{-\ell}+(8\ell T)/2^n\).

(If PRF-Login* is easier to prove secure than PRF-Login, you might wonder why we bother with PRF-Login in the first place and not simply use PRF-Login*. The reason is that specifying a random function \(H\) requires specifying \(2^n\) bits, and so that would be a huge shared key. So PRF-Login* is not a protocol we can actually run but rather a hypothetical “mental experiment” that helps us in arguing about the security of PRF-Login.)

Proof of Claim 1: Let \(i_1,\ldots,i_{2T}\) be the nonces chosen by Bob and recieved by Alice in the first \(T\) iterations. That is, \(i_1\) is the nonce chosen by Bob in the first iteration while \(i_2\) is the nonce that Alice received in the first iteration (if Mallory doesn’t modify it then \(i_1=i_2\)). Similarly, \(i_3\) is the nonce chosen by Bob in the second iteration while \(i_4\) is the nonce received by Alice and so on and so forth. Let \(i\) be the nonce chosen in the \(T+1^{st}\) iteration in which Mallory tries to impersonate Alice. We claim that the probability that there exists some \(j\in\{1,\ldots,2T\}\) such that \(|i-i_j|<2\ell\) is at most \(8\ell T/2^n\). Indeed, let \(S\) be the union of all the intervals of the form \(\{ i_j-2\ell+1,\ldots, i_j+2\ell-1 \}\) for \(1 \leq j \leq 2T\). Since it’s a union of \(2T\) intervals each of length less than \(4\ell\), \(S\) contains at most \(8T\ell\) elements, so the probability that \(i\in S\) is \(|S|/2^n \leq (8T\ell)/2^n\). Now, if there does not exists a \(j\) such that \(|i-i_j|<2\ell\) then it means in particular that all the queries to \(H(\cdot)\) made by either Alice or Bob during the first \(T\) iterations are disjoint from the interval \(\{ i,i+1,\ldots,i+\ell-1 \}\). Since \(H(\cdot)\) is a completely random function, the values \(H(i),\ldots,H(i+\ell-1)\) are chosen uniformly and independently from all the rest of the values of this function. Since Mallory’s message \(y\) to Bob in the \(T+1^{st}\) iteration depends only on what she observed in the past, the values \(H(i),\ldots,H(i+\ell-1)\) are independent from \(y\), and hence under the condition that there is no overlap between this interval and prior queries, the probability that they equal \(y\) is \(2^{-\ell}\). QED (Claim 1).

The proof of Claim 1 is not hard but it is somewhat subtle, so it’s good to go over it again and make sure you understand it.

Now that we have Claim 1, the proof of the theorem follows as outlined above. We build an adversary \(A\) to the pseudorandom function generator from \(M\) by having \(A\) simulate “inside its belly” all the parties Alice, Bob and Mallory and output \(1\) if Mallory succeeds in impersonating. Since we assumed \(\epsilon\) is non-negligible and \(T\) is polynomial, we can assume that \((8\ell T)/2^n < \epsilon/2\) and hence by Claim 1, if the black box is a random function, then we are in the PRF-Login* setting and Mallory’s success will be at most \(2^{-\ell}+\epsilon/2\). If the black box is \(f_s(\cdot)\), then we get exactly the PRF-Login setting and hence under our assumption the success will be at least \(2^{-\ell}+\epsilon\). We conclude that the difference in probability of \(A\) outputting \(1\) between the random and pseudorandom case is at least \(\epsilon/2\) thus contradicting the security of the pseudorandom function generator.

Modifying input and output lengths of PRFs

In the course of constructing this one-time-password scheme from a PRF, we have actually proven a general statement that is useful on its own: that we can transform standard PRF which is a collection \(\{ f_s \}\) of functions mapping \(\{0,1\}^n\) to \(\{0,1\}\), into a PRF where the functions have a longer output \(\ell\). Specifically, we can make the following definition:

Let \(\ell_{\text{in}},\ell_{\text{out}}:\N \rightarrow \N\). An ensemble of functions \(\{ f_s \}_{s\in \{0,1\}^*}\) is a PRF ensemble with input length \(\ell_{\text{in}}\) and output length \(\ell_{\text{out}}\) if:

  1. For every \(n\in\N\) and \(s \in \{0,1\}^n\), \(f_s:\{0,1\}^{\ell_{\text{in}}} \rightarrow \{0,1\}^{\ell_{\text{out}}}\).

  2. For every polynomial \(p\) and \(p(n)\)-time adversary \(A\), if \(n\) is large enough then

\[ \left| \E_{s\in\{0,1\}^n}[ A^{f_s(\cdot)}(1^n)] - \E_{h \leftarrow_R \{0,1\}^{\ell_{\text{in}}} \rightarrow \{0,1\}^{\ell_{\text{out}}} }[A^h(1^n)] \right| < 1/p(n) \;.\]

Standard PRFs as we defined in Definition 4.3 correspond to generalized PRFs where \(\ell_{\text{in}}(n)=n\) and \(\ell_{\text{out}}(n)=1\) for all \(n\in\N\). It is a good exercise (which we will leave to the reader) to prove the following theorem:

Suppose that PRFs exist. Then for every constant \(c\) and polynomial-time computable functions \(\ell_{\text{in}},\ell_{\text{out}}:\N \rightarrow \N\) with \(\ell_{\text{in}}(n), \ell_{\text{out}}(n) \leq n^c\), there exist a PRF ensemble with input length \(\ell_{\text{in}}\) and output length \(\ell_{\text{out}}\).

Thus from now on whenever we are given a PRF, we will allow ourselves to assume that it has any polynomial output size that is convenient for us.

Message Authentication Codes

One time passwords are a tool allowing you to prove your identity to, say, your email server. But even after you did so, how can the server trust that future communication comes from you and not from some attacker that can interfere with the communication channel between you and the server (so called “man in the middle” attack)? Similarly, one time passwords may allow a software company to prove their identity before they send you a software update, but how do you know that an attacker does not change some bits of this software update on route between their servers and your device?

This is where Message Authentication Codes (MACs) come into play- their role is to authenticate not only the identity of the parties but also their communication. Once again we have Alice and Bob, and the adversary Mallory who can actively modify messages (in contrast to the passive eavesdropper Eve). Similar to the case to encryption, Alice has a message \(m\) she wants to send to Bob, but now we are not concerned with Mallory learning the contents of the message. Rather, we want to make sure that Bob gets precisely the message \(m\) sent by Alice. Actually this is too much to ask for, since Mallory can always decide to block all communication, but we can ask that either Bob gets precisely \(m\) or he detects failure and accepts no message at all. Since we are in the private key setting, we assume that Alice and Bob share a key \(k\) that is unknown to Mallory.

What kind of security would we want? We clearly want Mallory not to be able to cause Bob to accept a message \(m'\neq m\). But, like in the encryption setting, we want more than that. We would like Alice and Bob to be able to use the same key for many messages. So, Mallory might observe the interactions of Alice and Bob on messages \(m_1,\ldots,m_T\) before trying to cause Bob to accept a message \(m'_{T+1} \neq m_{T+1}\). In fact, to make our notion of security more robust, we will even allow Mallory to choose the messages \(m_1,\ldots,m_T\) (this is known as a chosen message or chosen plaintext attack). The resulting formal definition is below:

Let \((S,V)\) (for sign and verify) be a pair of efficiently computable algorithms where \(S\) takes as input a key \(k\) and a message \(m\), and produces a tag \(\tau \in \{0,1\}^*\), while \(V\) takes as input a key \(k\), a message \(m\), and a tag \(\tau\), and produces a bit \(b\in\{0,1\}\). We say that \((S,V)\) is a Message Authentication Code (MAC) if:

  • For every key \(k\) and message \(m\), \(V_k(m,S_k(m))=1\).
  • For every polynomial-time adversary \(A\) and polynomial \(p(n)\), it is with less than \(1/p(n)\) probability over the choice of \(k\leftarrow_R\{0,1\}^n\) that \(A^{S_k(\cdot)}(1^n)=(m',\tau')\) such that \(m'\) is not one of the messages \(A\) queries and \(V_k(m',\tau')=1\).3

If Alice and Bob share the key \(k\), then to send a message \(m\) to Bob, Alice will simply send over the pair \((m,\tau)\) where \(\tau = S_k(m)\). If Bob receives a message \((m',\tau')\), then he will accept \(m'\) if and only if \(V_k(m',\tau')=1\). Mallory now observes \(t\) rounds of communication of the form \((m_i,S_k(m_i))\) for messages \(m_1,\ldots,m_t\) of her choice, and her goal is to try to create a new message \(m'\) that was not sent by Alice, but for which she can forge a valid tag \(\tau'\) that will pass verification. Our notion of security guarantees that she’ll only be able to do so with negligible probability, in which case the MAC is CMA-secure.4

The notion of a “chosen message attack” might seem a little “over the top”. After all, Alice is going to send to Bob the messages of her choice, rather than those chosen by her adversary Mallory. However, as cryptographers have learned time and again the hard way, it is better to be conservative in our security definitions and think of an attacker that has as much power as possible. First of all, we want a message authentication code that will work for any sequence of messages, and so it’s better to consider this “worst case” setting of allowing Mallory to choose them. Second, in many realistic settings an adversary could have some effect on the messages that are being sent by the parties. This has occurred time and again in cases ranging from web servers to German submarines in World War II, and we’ll return to this point when we talk about chosen plaintext and chosen ciphertext attacks on encryption schemes.

Some texts (such as Boneh Shoup) define a stronger notion of unforgability where the adversary cannot even produce new signatures for messages it has queried in the attack. That is, the adversary cannot produce a valid message-signature pair that it has not seen before. This stronger definition can be useful for some applications. It is fairly easy to transform MACs satisfying Definition 4.8 into MACs satisfying strong unforgability. In particular, if the signing function is deterministic, and we use a canonical verifier algorithm where \(V_k(m,\sigma)=1\) iff \(S_k(m)=\sigma\) then weak unforgability automatically implies strong unforgability since every message has a single signature that would pass verification (can you see why?).

MACs from PRFs

We now show how pseudorandom function generators yield message authentication codes. In fact, the construction is so immediate that much of the more applied cryptographic literature does not distinguish between these two concepts, and uses the name “Message Authentication Codes” to refer to both MAC’s and PRF’s. However, since this is not applied cryptographic literature, the distinction is rather important.

Under the PRF Conjecture, there exists a secure MAC.

Let \(F(\cdot,\cdot)\) be a secure pseudorandom function generator with \(n/2\) bits output (which we can obtain using Theorem 4.7). We define \(S_k(m) = F(k,m)\) and \(V_k(m,\tau)\) to output \(1\) iff \(F(k,m)=\tau\). Suppose towards the sake of contradiction that there exists an adversary \(A\) breaks the security of this construction of a MAC. That is, \(A\) queries \(S_k(\cdot)\) \(poly(n)\) many times and with probability \(1/p(n)\) for some polynomial \(p\) outputs \((m',\tau')\) that she did not ask for such that \(F(k,m')=\tau'\).

We use \(A\) to construct an adversary \(A'\) that can distinguish between oracle access to a PRF and a random function by simulating the MAC security game inside \(A'\). Every time \(A\) requests the signature of some message \(m\), \(A'\) returns \(O(m)\). When \(A\) returns \((m', \tau')\) at the end of the \(\ensuremath{\mathit{MAC}}\) game, \(A'\) returns \(1\) if \(O(m') = \tau'\), and \(0\) otherwise. If \(O(\cdot) = H(\cdot)\) for some completely random function \(H(\cdot)\), then the value \(H(m')\) would be completely random in \(\{0,1\}^{n/2}\) and independent of all prior queries. Hence the probability that this value would equal \(\tau'\) is at most \(2^{-n/2}\). If instead \(O(\cdot) = F(k,\cdot)\), then by the fact that \(A\) wins the MAC security game with probability \(1/p(n)\), the adversary \(A'\) will output \(1\) with probability \(1/p(n)\). That means that such an adversary \(A'\) can distinguish between an oracle to \(F(k,\cdot)\) and an oracle to a random function \(H\), which gives us a contradiction.

Arbitrary input length extension for MACs and PRFs

So far we required the message to be signed \(m\) to be no longer than the key \(k\) (i.e., both \(n\) bits long). However, it is not hard to see that this requirement is not really needed. If our message is longer, we can divide it into blocks \(m_1,\ldots,m_t\) and sign each message \((i,m_i)\) individually. The disadvantage here is that the size of the tag (i.e., MAC output) will grow with the size of the message. However, even this is not really needed. Because the tag has length \(n/2\) for length \(n\) messages, we can sign the tags \(\tau_1,\ldots,\tau_t\) and only output those. The verifier can repeat this computation to verify this. We can continue this way and so get tags of \(O(n)\) length for arbitrarily long messages. Hence in the future, whenever we need to, we can assume that our PRFs and MACs can get inputs in \(\{0,1\}^*\) — i.e., arbitrarily length strings.

We note that this issue of length extension is actually quite a thorny and important one in practice. The above approach is not the most efficient way to achieve this, and there are several more practical variants in the literature (see Boneh-Shoup Sections 6.4-6.8). Also, one needs to be very careful on the exact way one chops the message into blocks and pads it to an integer multiple of the block size. Several attacks have been mounted on schemes that performed this incorrectly.

Aside: natural proofs

Pseudorandom functions play an important role in computational complexity, where they have been used as a way to give “barrier results” for proving results such as \(\mathbf{P}\neq \mathbf{NP}\).5 Specifically, the Natural Proofs barrier for proving circuit lower bounds says that if strong enough pseudorandom functions exist, then certain types of arguments are bound to fail. These are arguments which come up with a property \(\ensuremath{\mathit{EASY}}\) of a Boolean function \(f:\{0,1\}^n \rightarrow \{0,1\}\) such that:

  • If \(f\) can be computed by a polynomial sized circuit, then it has the property \(\ensuremath{\mathit{EASY}}\).

  • The property \(\ensuremath{\mathit{EASY}}\) fails to hold for a random function with high probability.

  • Checking whether \(\ensuremath{\mathit{EASY}}\) holds can be done in time polynomial in the truth table size of \(f\). That is, in \(2^{O(n)}\) time.

A priori these technical conditions might not seem very “natural” but it turns out that many approaches for proving circuit lower bounds (for restricted families of circuits) have this form. The idea is that such approaches find a “non generic” property of easily computable function, such as finding some interesting correlations between the some input bits and the output. These are correlations that are unlikely to occur in random functions. The lower bound typically follows by exhibiting a function \(f_0\) that does not have this property, and then using that to derive that \(f_0\) cannot be efficiently computed by this particular restricted family of circuits.

The existence of strong enough pseudorandom functions can be shown to contradict the existence of such a property \(\ensuremath{\mathit{EASY}}\), since a pseudorandom function can be computed by a polynomial sized circuit, but it cannot be distinguished from a random function. While a priori a pseudorandom function is only secure for polynomial time distinguishers, under certain assumptions it might be possible to create a pseudorandom function with a seed of size, say, \(n^5\), that would be secure with respect to adversaries running in time \(2^{O(n^2)}\).

  1. We will often identify the strings of length \(n\) with the numbers between \(0\) and \(2^{n-1}\), and switch freely between the two representations, and hence can think of \(i\) also as a string in \(\{0,1\}^n\). We will also switch between indexing strings starting from \(0\) and starting from \(1\) based on convenience.

    ↩

  2. This also allows us to be consistent with the notion of “polynomial in the size of the input.”

    ↩

  3. Clearly if the adversary outputs a pair \((m,\tau)\) that it did query from its oracle then that pair will pass verification. This suggests the possibility of a replay attack whereby Mallory resends to Bob a message that Alice sent him in the past. As above, one can thwart this by insisting the every message \(m\) begins with a fresh nonce or a value derived from the current time.

    ↩

  4. A priori you might ask if we should not also give Mallory an oracle to \(V_k(\cdot)\) as well. After all, in the course of those many interactions, Mallory could also send Bob many messages \((m',\tau')\) of her choice, and observe from his behavior whether or not these passed verification. It is a good exercise to show that adding such an oracle does not change the power of the definition, though we note that this is decidedly not the case in the analogous question for encryption.

    ↩

  5. This discussion has more to do with computational complexity than cryptography, and so can be safely skipped without harming understanding of future material in this course.

    ↩

Comments

Comments are posted on the GitHub repository using the utteranc.es app. A GitHub login is required to comment. If you don't want to authorize the app to post on your behalf, you can also comment directly on the GitHub issue for this page.

Compiled on 11/17/2021 22:36:03

Copyright 2021, Boaz Barak. Creative Commons License
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Produced using pandoc and panflute with templates derived from gitbook and bookdown.